2024 - Catégorie "Excellence scientifique" : Cyriac Delie
Titre : Modélisation de systèmes dynamiques par les équations différentielles latentes
Promotrice : Annick Sartenaer
Copromotrice : Noémie Vlaminck (Cenaero)
Encadrant : Cédric Simal
Résumé :
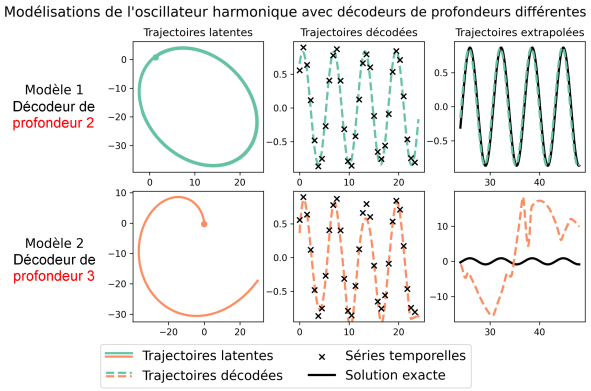
La modélisation de séries temporelles est une problématique récurrente dans de nombreux domaines tels que l’optimisation industrielle ou l’épidémiologie. Dans ce travail réalisé en collaboration avec Cenaero et Carmeuse Technologies, nous étudions la capacité du modèle d’équation différentielle latente (EDL) à reconstruire un système dynamique sur base de séries temporelles. L’objectif y est de pouvoir fournir un modèle cohérent respectant certaines propriétés, à savoir celles des systèmes dynamiques. L’EDL associe une équation différentielle neuronale, livrant la cohérence “dynamique” attendue, à des éléments issus des modèles génératifs, livrant une flexibilité souvent nécessaire pour répondre au problème de modélisation. Si l’EDL peut parvenir à une modélisation convenable, il apparaıt néanmoins que celle-ci soit sensible aux puissances respectives de ses deux composantes. Une composante générative trop puissante pourrait prendre le pas sur la composante dynamique, nuisant de ce fait à la cohérence du modèle, là où trop peu de puissance pourrait totalement entraver son fonctionnement. Il s’ensuit que l’EDL devrait être améliorée à cet égard, en contraignant la composante dynamique sans pour autant en limiter directement la puissance. Une solution pourrait être l’ajout d’un terme de régularisation au critère d’entraınement du modèle, afin d’amener à la conservation des propriétés topologiques en son sein.
2023 - Catégorie "Excellence scientifique" : Marie Dorchain
Titre : Motifs de Turing sur réseaux : étude des cas dirigés et dégénérés
Promoteur : Timoteo Carletti
Copromoteur : Riccardo Muolo
Résumé :
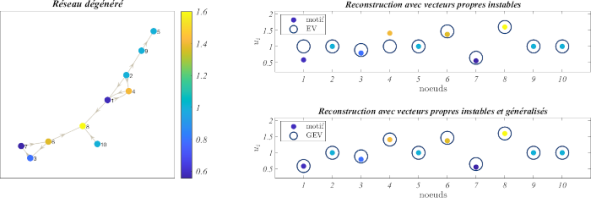
Les motifs font partie intégrante de ce qui nous entoure ; on peut notamment les retrouver sur les peaux des animaux par exemple, sur les coquillages, ou encore dans la distribution spatiale des produits d’une réaction chimique. Une des théories les plus répandues pour expliquer l’émergence de ces motifs est très certainement celle de Turing. En effet, en 1952, Alan Turing étudie un système de réaction-diffusion, c’est-à-dire un système où deux espèces sont en interaction et diffusent à travers le domaine; il suppose qu’un tel système possède un équilibre stable et, une fois perturbé, sous certaines conditions, le système peut atteindre un nouvel état inhomogène, qui est appelé motif de Turing. Si cette théorie a d’abord été étudiée pour un domaine continu, elle a ensuite été étendue aux domaines discrets, qui peuvent être modélisés à l’aide des réseaux. Plusieurs types de réseaux ont alors été considérés : dans un premier temps les réseaux non dirigés, ensuite dirigés et non-normaux.
Ce mémoire reprend donc les bases nécessaires de la théorie de Turing et reproduit les résultats établis pour les réseaux. Nous allons ensuite au-delà du cadre déjà étudié dans la littérature et considérons les réseaux dégénérés, dont la matrice Laplacienne ne possède pas de base de vecteurs propres, nécessaire à la théorie. Nous introduisons alors un nouveau formalisme permettant l’étude de la théorie de Turing sur un tel support. Nous nous intéressons aussi, dans un second temps, à la reconstruction de motifs. En effet, s’il a déjà été établi que le motif pouvait être expliqué grâce aux vecteurs propres de la matrice Laplacienne associée aux valeurs propres instables, nous nous intéressons spécialement à l’effet des vecteurs propres généralisés dans la reconstruction du motif.
2022 - Catégorie "Vulgarisation scientifique" : François-Grégoire Biewart
Titre : Étude d'une méthode numérique pour l'approximation du bassin d'attraction de systèmes dynamiques non linéaires au moyen de l'opérateur de Koopman
Promoteur : Alexandre Mauroy
Résumé :
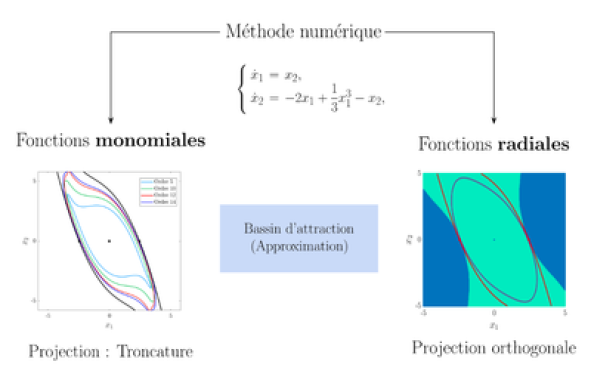
Dans la théorie des systèmes dynamiques non linéaires, l'étude de la stabilité globale de points fixes est un sujet loin d'être évident. En effet, la stabilité de tels attracteurs nécessite en général de déterminer une fonction de Lyapunov particulière parmi une infinité de choix possibles, ce qui peut devenir assez fastidieux. Ce constat motive alors une approche fonctionnelle des systèmes dynamiques via l'opérateur de Koopman. Dans ce contexte, la stabilité de points fixes repose sur l'existence de fonctions propres particulières de l'opérateur dont le support délimite les frontières du bassin d'attraction de l'équilibre. Cet opérateur étant de dimension infinie, le calcul analytique de ses fonctions propres n'est malheureusement pas trivial et nous devons en général en déterminer une approximation sur un sous-espace fini, engendré par certaines fonctions de base. Dans ce cas, l'approximation des fonctions propres est obtenue en calculant les vecteurs propres de la représentation matricielle de l'opérateur projeté dans la base choisie. Une base naturelle et souvent utilisée dans la littérature est celle des monômes pour laquelle il est possible de caractériser l’erreur d’approximation entre les fonctions propres exactes et estimées.
Dans ce mémoire, nous investiguons en particulier l'impact de la projection et du choix de la base sur l'approximation du bassin d'attraction. Pour ce faire, nous développons une méthode numérique générale, que nous appliquons avec des fonctions de base radiales et monomiales sur différents systèmes, notamment en trois dimensions. Nous montrons que l'utilisation de ces fonctions fournit une bonne estimation du bassin d'attraction en particulier pour des fonctions de base radiales qui n'avaient pas encore été considérées dans ce contexte. En parallèle, nous traitons également certaines questions théoriques découlant de cette étude, ce qui permet notamment d’obtenir des garanties de stabilité rigoureuses, malgré les approximations effectuées.
2022 - Catégorie "Excellence scientifique" : Gaetan Louvet
Titre : Robustesse : fonction d’influence de la profondeur de demi-espace scatter et du graphical lasso
Promoteur : Germain Van Bever
Résumé :
Lorsque nous recevons un jeu de données à analyser, il peut arriver que des valeurs aberrantes apparaissent, impactant alors les méthodes statistiques utilisées. Il existe différents outils permettant d'évaluer la robustesse de procédures, c'est-à-dire leur sensibilité lorsque les données sont contaminées. Ce récit s'intéresse à la robustesse de plusieurs méthodes statistiques. Dans le premier chapitre, nous commençons par définir différents outils afin d'évaluer la robustesse. Ensuite, nous introduisons les estimateurs robustes de position et de dispersion les plus connus et les plus utilisés. Dans le second chapitre, nous nous intéressons aux fonctions de profondeur, qui permettent de quantifier la centralité d'une valeur pour un certain paramètre. Nous discutons en particulier de la profondeur de demi-espace de position et de scatter. Après introduction de ces différents concepts, nous dérivons la fonction d'influence de la profondeur scatter. Nous commençons en considérant que l'estimateur de position dont cette dernière dépend est connu et fixé. Nous nous intéressons ensuite au cas où la distribution est discrète à support fini, et nous concluons enfin en donnant des bornes pour la fonction d'influence dans le cas où la distribution est absolument continue par rapport à la mesure de Lebesgue.
2021 - Catégorie "Vulgarisation scientifique" : Célestine Hiernaux
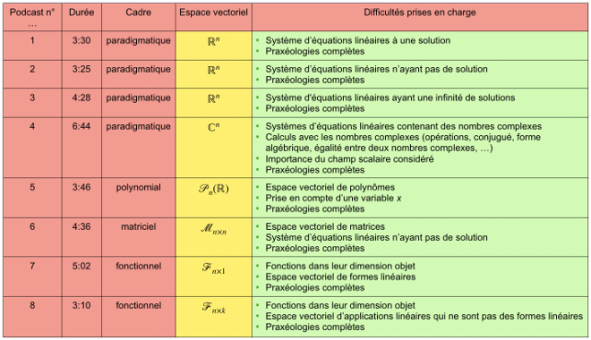
Titre : Des podcasts sur les combinaisons linéaires: Illustration du caractère unificateur de l’algèbre linéaire… et bien plus encore!
Promoteur : Martine De Vleeschouwer
Résumé :
Le caractère unificateur de l’algèbre linéaire n’est pas facilement identifié par les étudiants débutants dans ce domaine. Dans le cadre de ce mémoire, nous avons créé un dispositif qui consiste en une proposition d’une série de podcasts illustrant la notion algébrique de combinaison linéaire. Cette notion est assez élémentaire pour que les débutants puissent l’appliquer à des espaces vectoriels différents, de manière progressive, de façon à mettre en lumière ce caractère unificateur. Les spécificités d’enseignement et d’apprentissage de l’algèbre linéaire, comme l’obstacle du formalisme, se mêlent aux difficultés déjà repérées dans la littérature. Certaines sont prises en charge de manière évolutive par le dispositif comme les difficultés à résoudre et interpréter des systèmes d’équations linéaires, à travailler avec des nombres complexes et à considérer les fonctions comme des «objets» mathématiques, en tant qu’éléments d’une structure algébrique. La justification de toute technique utilisée par un discours théorique pose également souvent problème aux étudiants dans la transition secondaire/université. Tous les podcasts montrent donc l’importance de la théorie et de la rigueur mathématique dans les exercices pour faciliter l’apprentissage du domaine de l’algèbre linéaire. Ce travail de création de liens entre la théorie et les exercices est souvent réalisé en autonomie par les étudiants. Les podcasts, qui agiraient comme un complément aux cours, pourraient leur être utiles. Le dispositif a été testé auprès d’étudiants débutants en algèbre linéaire et des enquêtes leur ont été envoyées. Des contraintes institutionnelles dues à l’organisation de la mise en oeuvre du dispositif et des contraintes sanitaires dues au Covid-19 ont empêché une analyse significative des résultats à ces enquêtes. Nous en avons également proposé une aux assistants et collaborateurs didactiques des séances d’exercices de ce public test. Les réponses récoltées nous ont permis d’obtenir des avis positifs sur le projet de ce mémoire, de tirer des conclusions et de rassembler des pistes d’amélioration et des perspectives possibles.
Le projet en vidéo :
1. Combinaisons linéaires dans R^n - vidéo1
2. Combinaisons linéaires dans R^n - vidéo2
3. Combinaisons linéaires dans R^n - vidéo 3
4. Combinaisons linéaires dans C^n
5. Combinaisons linéaires dans les Polynômes
6. Combinaisons linéaires dans les Matrices
7. Combinaisons linéaires dans les Applications - vidéo1
8. Combinaisons linéaires dans les Applications - vidéo2
2021 - Catégorie "Excellence scientifique" : Martin Baptiste
Titre : La théorie de Galois aujourd’hui.
Promoteur : Alexandre Mauroy
Résumé :
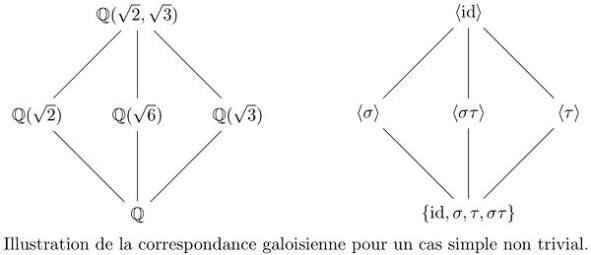
La théorie de Galois sous sa forme moderne est souvent résumée en deux théorèmes ayant eu une influence considérable sur la manière d'aborder les problèmes de l'algèbre. Le premier est la correspondance galoisienne, le second est la condition nécessaire et suffisante de résolubilité d'une équation polynomiale par radicaux. Motivés par l'efficacité et la profondeur de ces derniers, les mathématiciens se sont efforcés de généraliser et de transposer ces théorèmes à d'autres branches des mathématiques. Ainsi, si les applications les plus connues de cette théorie semblent quelque peu surannées, on trouvera aujourd'hui une remarquable diversité de nouvelles correspondances galoisiennes offrant une myriade de solutions et aussi de problèmes ouverts aux géomètres de notre époque.
Ce mémoire s'inscrit donc davantage comme un résumé non-exhaustif des différents sujets dans lesquels la théorie de Galois interfère que comme une véritable présentation rigoureuse de toute cette théorie. Le premier chapitre est consacré à la théorie de Galois classique, celle développée par Galois, mais sous sa forme moderne. Ce dernier est plus complet que les chapitres suivants car il est à la base de tous ceux qui le succèdent. L'objectif visé est de formuler une présentation plus simple que ce que l'on peut trouver dans les livres ou dans les cours connus de cette théorie et de démystifier certains points pour les néophytes. Ainsi, j'espère exposer une approche que j'aurais aimé avoir lue lors de mes premiers contacts avec la théorie de Galois. Le deuxième chapitre aborde la théorie de Galois infinie, un premier prolongement de la théorie de Galois classique aux extensions algébriques de degré infini. Cette théorie, pourtant importante, est assez peu exposée dans les livres sur la théorie de Galois et le but de cette section est de coupler la théorie quelque peu abstraite avec des exemples assez concrets. Le troisième exhibe les liens entre l'arithmétique des extensions du corps des rationnels et le groupe de Galois associé. Ce chapitre explicite comment la théorie de Galois s'applique naturellement à une théorie plus ancienne qu'elle : La théorie des nombres. Le quatrième présente succinctement la théorie de Galois différentielle. Celle-ci possède de nombreuses analogies avec le premier chapitre, mais l'objet principal de cette section est l'équation différentielle linéaire. Le cinquième chapitre porte sur la théorie de Galois des revêtements, une théorie qui montre qu'il existe une correspondance galoisienne entre revêtements et sous-groupes du groupe fondamental de l'espace topologique de base.
2020 - Catégorie "Vulgarisation scientifique" et "Excellence scientifique" : Judicaël Mohet
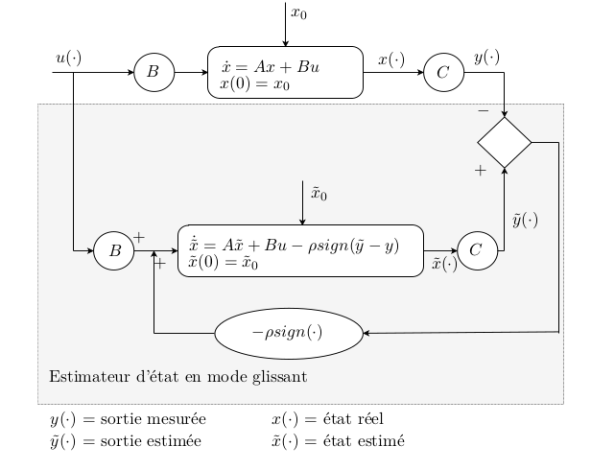
Titre : Estimation par mode glissant de l'état d'un système de convection-diffusion-réaction linéaire.
Promoteur : Joseph Winkin & Encadrant : Anthony Hastir
Résumé :
L’estimation d’état en dimension infinie reste à ce jour un véritable défi. Le principe est d’approcher les trajectoires d’état d’un système dynamique sur base de son entrée et de sa sortie. Dans le cas d’un espace d’état de dimension infinie, il faut également démontrer le caractère bien posé du système ainsi que de l’estimateur. Une méthode d’estimation robuste consiste à appliquer une entrée discontinue sur la dynamique d’erreur, ce qui permet d’emprisonner les trajectoires dans ce qu’on appelle une surface de glissement. Cette technique porte le nom d’estimation par mode glissant et son plus grand avantage est de pouvoir compenser des perturbations bornées qui agissent sur le système. Dans ce mémoire, un tel estimateur est appliqué en dimensions finie et infinie sur un modèle de convection-diffusion-réaction linéaire soumis à une perturbation bornée. Celui-ci décrit l’évolution de divers processus industriels tels que des réacteurs chimiques ou biochimiques. En utilisant une approche fonctionnelle, le caractère bien posé de l’estimateur est établi en démontrant la génération de semi-groupe fortement continu et compact sur l’espace de Sobolev H1(0,1). Ensuite, la stabilité est prouvée via la théorie de Lyapunov. Enfin, une comparaison des performances de l’estimateur en dimension finie et en dimension infinie est effectuée grâce à des simulations numériques.
2019 - Catégorie "Vulgarisation scientifique" : Hugo Henris
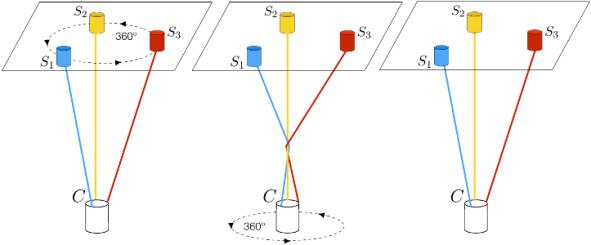
Titre : Formation du satellite multi-câblé avec les satellites adjoints en mouvement le long des courbes de Lissajous.
Promoteur : Anne Lemaître
Résumé :
En physique atmosphérique et géodésique de plasma, des mesures multi-points sont de plus en plus nécessaires. Encore plus dans le cadre de l’interférométrie spatiale, des mesures simultanées peuvent être effectuées à l’aide d’un ensemble de sondes connectées par des attaches alignées le long de la verticale locale. Dans le but de minimiser la consommation de fuel, il a été imaginé de relier ces satellites adjoints disposant de capteurs à un même satellite (et non entre eux) au moyen de câbles. La rotation et la force gravitationnelle ne suffisant pas, les satellites adjoints sont tout de même équipés de moteurs à faible poussée afin de garder les liens tendus entre les satellites. Ils permettent de stabiliser la dynamique souhaitée du système. Dans ce mémoire, la modélisation complète des équations du mouvement d'un tel système y est tout d'abord détaillée. Un des équilibres envisageable est également présenté, ainsi que les effets des faibles déviations autour de celui-ci. Une présentation théorique et numérique du mouvement des satellites le long des courbes de Lissajous est également proposée. La possibilité d’enchevêtrement de câbles est évidement présente, augmentant le risque de collisions et la complexité du déploiement d’un tel système. Ce mémoire contient donc une étude approfondie de ce risque. Tout d'abord en distinguant deux types d'enchevêtrements différents (faible et fort) et ensuite en identifiant les configurations plus sujettes à des risques que d'autres au moyen de théorèmes démontrés. Une série de nombre de satellites adjoints et de valeur de paramètres engendrant des enchevêtrements forts sont alors exclus. Enfin, l'étudie des effets de non linéarité du mouvement des satellites adjoints le long des courbes de Lissajous, supposé instable, est brièvement présenté.
Source de l'image : H. Henris, Formation du satellite multi-câblé avec les satellites adjoints en mouvement le long des courbes de Lissajous, Université de Namur, Juin 2019
2019 - Catégorie "Excellence scientifique" : Alice Bellière
Titre : Application de la théorie des limites de graphes aux systèmes dynamiques sur réseau de type réaction-diffusion et instabilité de Turing.
Promoteur : Timotéo Carletti & Encadrant : Julien Petit
Résumé :
Étudier un réseau et la dynamique qui opère sur celui-ci possède un grand intérêt puisque les processus rencontrés dans la nature ou les technologies peuvent souvent être modélisés aux moyens d'un réseau. Cependant, la complexité de tels réseaux, qui sont de plus en plus grands, empêche encore à ce jour d'obtenir certaines réponses. Nous inscrivons notre recherche dans la théorie des graphons qui définit un objet limite conservant en mémoire la structure du réseau. Nous appliquons cette théorie au cas de dynamique de réaction-diffusion incluant des cas d'instabilité de Turing, où l'équilibre stable de la réaction est instable pour la réaction-diffusion. Nous montrons que la solution sur réseau converge vers celle définie via un graphon, nous offrant une alternative à l'introduction de la dynamique sur un très grand graphe. Nous avons appliqué l’étude de la convergence de la solution sur réseau vers celle via graphon au cas à une espèce unique puis à deux espèces en interaction suivant le modèle Brusselator (voir figure ci-dessous pour un exemple). Cette approche par les graphons nous faisant gagner de la mémoire et du temps d'exécution, elle permet entre autres de connaitre plus facilement les motifs de Turing. Un autre avantage du graphon est la détermination relativement aisée de la stabilité et de la structure propre de l'opérateur graphon correspondant. Cet opérateur étant l'analogue en dimension infinie de la matrice Laplacienne du graphe, il nous permet d'éviter d'étudier la structure propre d'une matrice de grande dimension.
Source de l'image : A. Bellière, Application de la théorie des limites de graphes aux systèmes dynamiques sur réseau de type réaction-diffusion et instabilité de Turing, Université de Namur, Juin 2019
2018 : Anthony Hastir
Titre : Dynamical analysis of a nonisothermal axial dispersion reactor.
Promoteur : J. Winkin
Résumé :
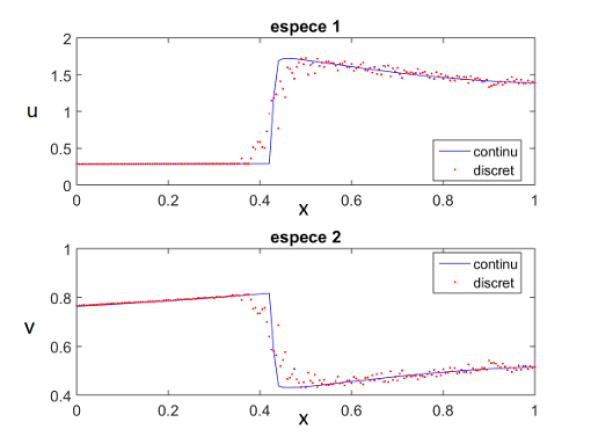
La conception d'une loi de contrôle afin de stabiliser la température et la concentration des composants chimiques lors d'une réaction dans un réacteur tubulaire non isotherme avec dispersion axiale reste encore un défi dans le milieu du génie des procédés. Des étapes préliminaires telles que le caractère bien posé, l'analyse de stabilité et l'analyse des équilibres d'un tel réacteur chimique sont alors cruciales. Dans ce mémoire, ces différentes étapes sont développées pour une réaction du type A -> B où A représente le réactif et B le produit. Ce type de système à paramètres répartis est régi par des équations aux dérivées partielles dites de réaction-convection-diffusion avec un terme non linéaire. Nous montrons d'abord que le système étudié est bien posé au moyen de la théorie des semi-groupes linéaires et non linéaires notamment. Ensuite, la stabilité exponentielle de la partie linéaire est prouvée. L'étape suivante est l'analyse des équilibres qui s'articule autour de deux nombres spécifiques, le nombre de Peclet massique et le nombre de Peclet thermique. Les analyses déjà présentes sont étendues dans le cas où ces deux nombres sont différents. Le résultat principal obtenu est que le réacteur peut exhiber un ou trois équilibres, notamment en fonction du coefficient de diffusion. De plus, des formes analytiques approchées des profils d'équilibre sont calculées explicitement au moyen de la théorie des perturbations. La dernière partie de ce mémoire traite de la stabilité des profils d'équilibre. Un modèle linéarisé autour des différents équilibres est construit et le caractère bien posé de celui-ci est démontré. En ce qui concerne l'étude de stabilité, diverses approches sont mises en oeuvre. Une méthode numérique connue sous le nom de méthode des résidus de Galerkin est notamment développée pour des nombres de Peclet égaux et étendue à des nombres de Peclet différents. Toutes les analyses et les résultats obtenus sont appuyés par des simulations numériques.
Source de l'image : A. Hastir, Dynamical analysis of a nonisothermal axial dispersion reactor, Université de Namur, Juin 2018
2017 - Arnaud Roisin
Titre : Développement d'un intégrateur symplectique pour les systèmes binaires. Application à la formation des systèmes de planètes géantes.
Promoteur : A.-S. Libert
Résumé :
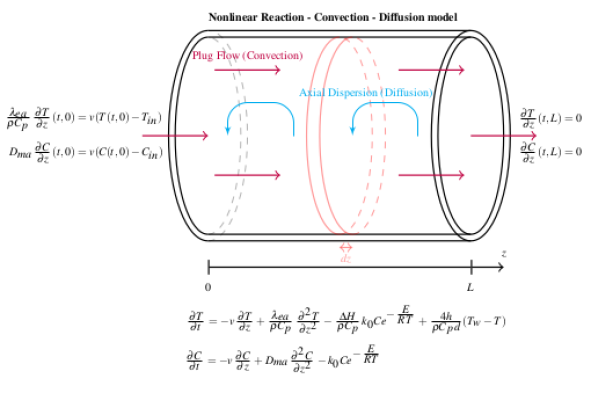
Actuellement, les scientifiques estiment que plus de la moitié des systèmes stellaires sont multiples. Des exoplanètes ont déjà été détectées dans une soixantaine de ces systèmes. Dans ce mémoire, nous avons développé un intégrateur symplectique calculant l'évolution des systèmes binaires abritant des planètes de type S, c'est-à-dire en orbite autour d'une des deux étoiles. L'intérêt de tels intégrateurs est de permettre, sur base de la structure hamiltonienne des équations d'évolution, de limiter la perte d'énergie, même avec un pas d'intégration élevé. L'adaptation du code existant SyMBA aux systèmes binaires a nécessité l'introduction d'un jeu de coordonnées adapté, ainsi qu'un découpage différent de l'hamiltonien. Notre code est également adapté au problème des rencontres proches entre les planètes et à celui des rencontres proches entre les planètes et le corps central. La question de la migration des systèmes de planètes géantes dans les binaires a ensuite été abordée. Le code a été modifié pour simuler la migration de type II des planètes géantes et étudier l'influence d'un compagnon binaire éloigné sur les configurations finales des corps. Pour ce faire, nous avons étudié l'évolution de plus de 1300 simulations. Notre attention s'est portée, en particulier, sur l'influence des paramètres initiaux du compagnon binaire sur le processus de migration.
Source de l'image : A. Roisin, Développement d'un intégrateur symplectique pour les systèmes binaires. Application à la formation des systèmes de planètes géantes., Université de Namur, Juin 2017
2016 : Elodie Mal & François Staelens
Elodie Mal
Titre : Etude de différents formalismes mathématiques en géométrie symplectique et conception d'un enseignement.
Promoteur : A.-S. Libert
Résumé :
La géométrie symplectique est une discipline mathématique étudiant les variétés différentiables munies d’une 2-forme fermée et non-dégénérée. Elle s’applique parfaitement à l’étude des espaces des phases des systèmes conservatifs et peut s’étudier selon trois formalismes mathématiques : les systèmes dynamiques, l’algèbre et la géométrie différentielle. Le cours de Géométrie symplectique SMATB307 enseigné en bachelier en sciences mathématiques à l’Université de Namur est orienté systèmes dynamiques. La question de la pertinence de proposer un enseignement plus axé géométrie différentielle se pose naturellement et est l’objet de ce travail. D’une part, ce mémoire présente une étude théorique de la géométrie symplectique dans les différents formalismes. Les concepts équivalents dans les formalismes dynamique, algébrique et différentiel sont mis en évidence afin de découvrir l’entrelacement des différents axes. D’autre part, un enseignement basé. sur le formalisme différentiel est conçu. Cet enseignement a été proposé aux étudiants en sciences mathématiques durant l’année académique 2015-2016 et l’avis de ces derniers sur le contenu de la séance a été analysé via un questionnaire. Ce mémoire a été rédigé avec un souci pédagogique constant.
Source de l'image : F. Staelens, Etude des variétés hilbertiennes et application à la mécanique quantique, Université de Namur, Juin 2016
François Staelens
Titre : Etude des variétés hilbertiennes et application à la mécanique quantique.
Promoteur : A. Füzfa
Résumé :
La géométrie différentielle en dimension infinie n’est généralement pas enseignée dans les cours universitaires mais elle est parfaitement développée de manière théorique et globale. Toutefois, l’écriture locale et le calcul tensoriel semblent avoir été mis de côté au profit des résultats globaux. Les variétés hilbertiennes, variétés dont l’espace de représentation est un espace de Hilbert séparable, semblent pourtant pouvoir potentiellement jouer un rôle en physique théorique. La mécanique quantique utilise en effet des espaces de Hilbert, alors que la relativité générale est construite sur la géométrie riemannienne. Ceci motive l’étude des variétés hilbertiennes accomplie dans ce mémoire. Une présentation détaillée des concepts généraux de géométrie différentielle en dimension infinie est réalisée. De plus, ce travail s’intéresse de près à l’écriture locale et au calcul tensoriel. La plupart des formules tensorielles utilisées en géométrie différentielle et riemannienne sont développées dans le cas hilbertien. Pour terminer, une tentative d’application à la mécanique quantique est présentée. Cet essai fait ressortir un problème de fond : la mécanique quantique est profondément linéaire alors que la géométrie différentielle est, par nature, non linéaire. Ce mémoire est à la fois une étude bibliographique et une recherche exploratoire.
Source de l'image : F. Staelens, Etude des variétés hilbertiennes et application à la mécanique quantique, Université de Namur, Juin 2016

2015 : François Lamoline
Titre : Analyse et contrôle LQ-optimal de systèmes hamiltoniens à ports.
Promoteur : J. Winkin
Résumé :
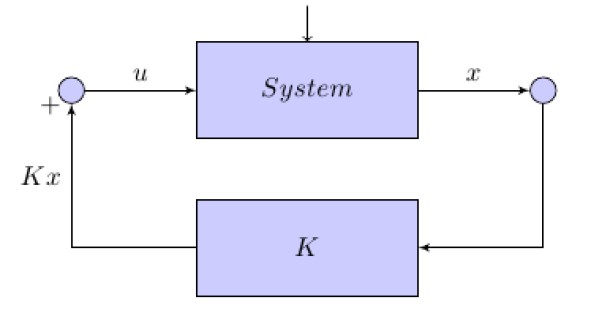
Dans ce mémoire, Nous nous intéressons aux systèmes hamiltoniens à ports en dimension infinie. Cette approche hamiltonienne à ports nous permet de considérer une large gamme de problèmes impliquant du contrôle aux frontières du domaine spatial. L'intérêt premier de cette formulation hamiltonienne à ports est la structure du modèle mathématique obtenu. Celle-ci nous permet de développer une analyse plus appropriée que l'approche semi-groupe qui peut, certes, être employée pour tout système dynamique de dimension infinie mais s'avère dans certains cas difficile à mettre en oeuvre.
Les systèmes hamiltoniens à ports sont des systèmes dynamiques sur lesquels les entrées agissent aux frontières du domaine spatial. Les sorties sont également mesurées au niveau des frontières. Nous montrerons qu'il est possible de caractériser les entrées et sorties par des matrices. Ces matrices seront utilisées pour étudier des propriétés pour cette classe de systèmes comme l'existence et l'unicité d'une solution, la stabilité et, pour en déterminer l'équation d'équilibre. Nous montrerons également que la classe des systèmes hamiltoniens à ports est une sous-classe des systèmes spectraux de Riesz. Enfin, nous étudierons la commande linéaire quadratique d'un système hamiltonien à ports. Tout au long de ce mémoire, nous appliquons la théorie présentée à l'exemple d'une corde vibrante.
Source de l'image : F. Lamoline, Analysis and linear-quadratic optimal control of port-hamiltonian systems , report naXys-10-2015, Université de Namur, Août 2015
2014 : Gwendoline Planchon & Manon Bataille
Gwendoline Planchon
Titre : Formation de motifs dans les modèles biologiques.
Promoteur : T. Carletti
Résumé :
De nombreux motifs sont présents dans la nature et ont poussé les chercheurs à vouloir modéliser la pigmentation. Les modèles utilisés dans ce travail considèrent des systèmes d'équations différentielles partielles incluant le processus de réaction-diffusion-advection. Certaines conditions permettant la formation de motifs ont été données par Alan Turing en 1952 et s'appellent depuis lors les instabilités de Turing. Nous étudions dans ce mémoire les dynamiques de réaction-diffusion-advection dans des domaines continus puis dans des réseaux (diffusion dans des réseaux en dimension d selon d directions indépendantes et diffusion dans les multiplex) et nous déterminons les conditions à imposer sur l'ensemble des paramètres pour avoir affaire à des instabilités de Turing. Nous mettons en évidence le rôle important de la discrétisation du domaine dans le développement ou non de motifs spatialement hétérogènes. Nous avons également déterminé l'ensemble des points de bifurcation donnant trois types différents de motifs (rayures, rectangles et hexagones) pour un modèle donné. Enfin, nous montrons que le couplage des niveaux d'un multiplex permet d'engendrer des instabilités de Turing qui ne sont pourtant permises sur aucune des couches prises séparément.
Source : G. Planchon, Formation de motifs dans les modèles biologiques , Université de Namur, Juin 2014

Manon Bataille
Titre : Importance des effets relativistes et de marée dans les systèmes binaires.
Co-promoteurs : A. Lemaître & A.-S. Libert
Résumé :
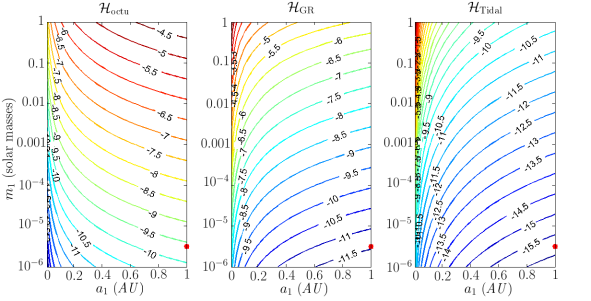
Les systèmes d'étoiles binaires représentent plus de la moitié de la population des étoiles. Des observations récentes ont montré que certains d'entre eux abritent une exoplanète. Dans ce travail, l'évolution à long terme des systèmes binaires possédant un compagnon planétaire ou stellaire est analysée au moyen du développement analytique octupole auquel sont ajoutés les effets relativistes et de marée (masses non ponctuelles).
Cette approche décrit avec précision la dynamique des systèmes triples hiérarchiques, quelles que soient les masses des différents corps. L'objectif de cette étude est de déterminer l'importance de ces deux corrections dans la dynamique des systèmes. En particulier, des cartes évaluant les ordres de grandeur de chaque contribution hamiltonienne sont élaborées pour un large éventail de masses et de demi-grand axes du deuxième corps, dans le cas des effets conservatifs. La question de la formation des systèmes binaires est également abordée, et ce dans l'optique de comprendre l'accumulation de compagnons planétaires de faible période (entre 1 et 10 jours). Une étude statistique de l'évolution séculaire de systèmes non coplanaires est réalisée, prenant en compte à la fois l'évolution orbitale et des spins des corps. Il s'ensuit que la combinaison du mécanisme de Kozai et des marées dissipatives est responsable de la migration des planètes vers de faibles périodes.
Source de l'image : M. Bataille, Importance des effets relativistes et de marée dans les systèmes binaires , Université de Namur, Juin 2014
2013 - Virginie Marelli
Titre : Matching on school choice: theory and algorithms.
Promoteur : T. Carletti, Co-promoteur : G. Aldashev
Résumé :
Dans ce mémoire, nous appliquons les algorithmes génétiques à des problèmes de matching. Dans un premier temps, nous passons en revue toute la théorie du matching, tant d'un point de vue économique que d'un point de vue algorithmique. Nous analysons trois problèmes de matching : le cas simple du one-to-one matching ou mariage; le many-to-one matching sans contrainte et le many-to-one matching avec contraintes. Dans un deuxième temps, nous décrivons brièvement les algorithmes génétiques, leur mode de fonctionnement et leurs adaptations. Nous les intégrons dans un problème simple de matching : le problème du mariage afin de les tester. Ensuite, nous les appliquons à un cas réel de répartition des élèves dans les écoles belges. Ce problème est sujet à des contraintes imposées par le décret "missions". Ce cas de many-to-one matching avec contraintes et indifférences n'a pas encore été traité dans la littérature existante et les algorithmes génétiques donnent de bons résultats. Dans un dernier temps, nous appliquons encore les algorithmes génétiques à un autre problème de matching : la formation de coalitions. Dans ce cas également, l'apport de ces algorithmes s'avère intéressant.
Source de l'image : V. Marelli, Matching on school choice : theory and algorithms, Université de Namur, Juin 2013
2012 - Estelle Collard
Titre : Mécanique quantique : une étude des équations de Schrödinger-Newton.
Promoteur : A. FÜZFA
Résumé :
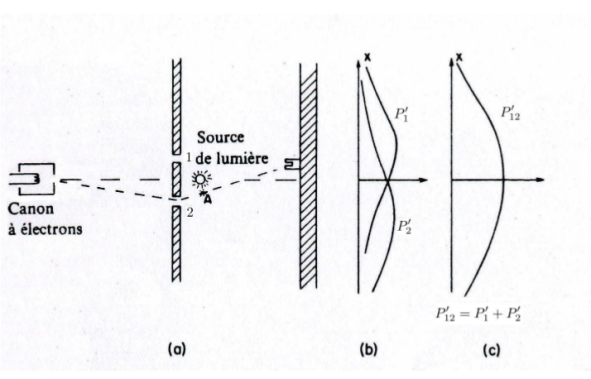
Ce mémoire se veut une étude des équations de Schrödinger-Newton (SN) dans le cas de deux particules. Ces équations de SN furent initialement introduites par Penrose pour remplacer la traditionnelle équation de Schrödinger et expliquer la décohérence de la fonction d'onde aux échelles macroscopiques. Penrose ajouta des auto-interactions gravitationnelles aux systèmes quantiques, au moyen d'une équation de Poisson, pour forcer cette décohérence.
Plusieurs études se sont déjà penchées sur les solutions des équations de SN, mais toujours dans le cas d'une seule particule. Quelques uns de leurs résultats numériques sont reproduits dans ce mémoire pour le cas de la symétrie sphérique. Ils montrent qu'il existe une infinité discrète de solutions stationnaires associées à des énergies de plus en plus élevées. La solution fondamentale présente l'énergie la plus faible et ne possède pas de zéro. D'autres papiers ont démontré que cet état fondamental est la seule solution stable. De manière générale, la n-ème solution possède n zéros et une énergie plus élevée.
Dans ce mémoire, l'influence de la masse a été étudiée et semble confirmer l'hypothèse de Penrose selon laquelle les équations de SN forment un lien entre les mondes quantiques et macroscopiques. En effet l'état fondamental, dimensionné selon la masse, montre que les objets lourds sont extrêmement bien localisés alors que les particules quantiques s'avèrent non localisées. La transition entre les mondes quantique et macroscopique se situe pour des masses de l'ordre de 10-18 kg.
Une étude pour deux particules a été commencée dans ce mémoire, bien que l'expression des équations de SN pour plusieurs particules soit sujette à discussion. Deux expressions sont donc étudiées ici. La première, proposée spécialement pour ce mémoire, s'inspire de la décomposition selon le centre de masse de l'équation de Schrödinger; décomposition à laquelle des auto-interactions sont ajoutées. La seconde expression provient de la formulation des équations de SN proposée par Diosi; et cette formulation n'a jamais été étudiée numériquement pour plusieurs particules. Ces deux approches furent considérées dans le cas de la symétrie sphérique. Différentes solutions stationnaires ont été trouvées, associées à des énergies de plus en plus grandes; la solution avec l'énergie la plus faible étant à nouveau l'état et l'ordre de grandeur semblables, bien que l'expression de Diosi présente une énergie plus faible et un état plus localisé.
Pour finir, une étude du système avec moment cinétique fut entreprise.
Sources de l'image : R. Feynman, R. Leighton et M.Sands, Mécanique quantique , InterEditions, Paris, 1992
E. Collard, Mécanique quantique : une étude des équations de Schrödinger-Newton, Université de Namur, Juin 2012
2011 - Romain Hendrickx
Titre : Les algorithmes génétiques : théorie et applications.
Promoteur : T. Carletti
Résumé :
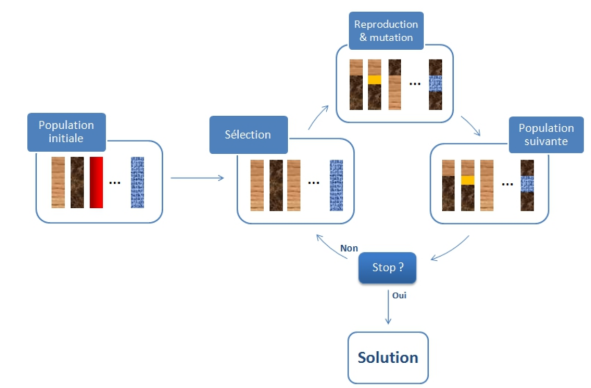
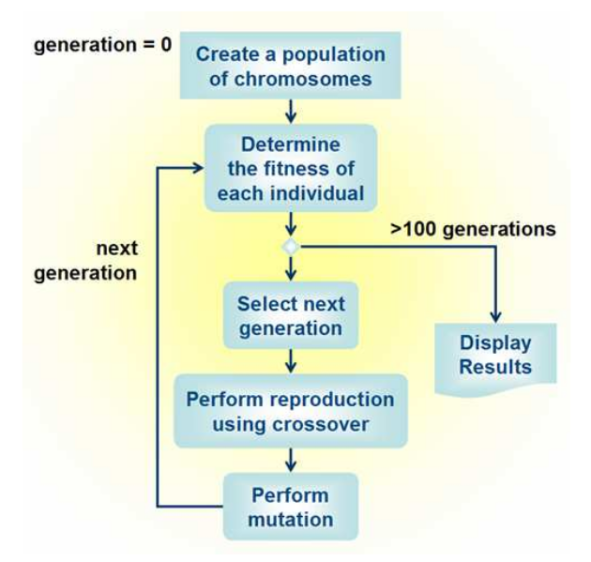
Les algorithmes génétiques (GAs) sont des méthodes de résolution méta-heuristiques pour les problèmes d'optimisation combinatoire, dont le fonctionnement est inspiré du processus d'évolution décrit par Darwin.
L'idée générale est de faire la comparaison entre les solutions admissibles du problème d'optimisation et un ensemble d'individus évoluant dans un monde abstrait, dans lequel leur adaptabilité est décrite par la fonction objectif, de telle manière à ce que plus la fonction objectif est grande et plus les individus sont "adaptés" à leur environnement. Dès lors, en partant d'une population initiale donnée et en simulant un processus d'évolution basé sur l'alternance d'opérateurs de variations, permettant d'explorer l'espace des solutions admissibles, et d'un opérateur de sélection, permettant de ne garder que les meilleurs individus (i.e. ayant la plus grande fitness), les algorithmes génétiques permettent d'obtenir au fil des générations un ensemble d'individus de plus en plus "adaptés à leur environnement", et donc par construction ayant une valeur objective de plus en plus proche de la solution optimale.
Le but de ce mémoire est de donner un aperçu du fonctionnement général des GAs. Une première partie du mémoire est consacrée à l'introduction de la structure générale des GAs, avec les spécifications les plus courantes pour les opérateurs de variation et de sélection (chapitre 1 et 2), ainsi qu'une justification théorique de leur utilisation (chapitre 3). La deuxième partie du mémoire est consacrée à l'application des GAs sur certains problèmes d'optimisation combinatoire. Nous étudions par exemple le problème de stratégie optimale d'un robot dont la tâche est de nettoyer une surface recouverte de canettes vides (connu sous le nom de "Robby, the Soda-Can-Collecting Robot", chapitre 4). Nous considérons également l'optimisation robuste des expériences par évènements dans le cadre de l'imagerie par résonance magnétique fonctionnelle (réalisé dans le cadre du stage de Master 2, chapitre 5).
Source de l'image : Source : R. Hendrickx, Les algorithmes génétiques : théorie et applications , Université de Namur, Juin 2011