2023 - "Scientific Excellence" category: Marie Dorchain
Title: Turing patterns on networks: a study of directed and degenerate cases
Promoter: Timoteo Carletti
Copromoter: Riccardo Muolo
Summary:
Patterns are an integral part of what surrounds us; they can be found on animal skins, for example, on shells, or even in the spatial distribution of the products of a chemical reaction. One of the most popular theories to explain the emergence of these patterns is undoubtedly that of Turing. In 1952, Alan Turing studied a reaction-diffusion system, i.e. a system in which two species interact and diffuse through the domain; he assumed that such a system possessed a stable equilibrium and, once disturbed, under certain conditions, the system could reach a new inhomogeneous state, which is called a Turing pattern. While this theory was first studied for a continuous domain, it was later extended to discrete domains, which can be modeled using networks. Several types of networks were then considered: initially undirected, then directed and non-normal.
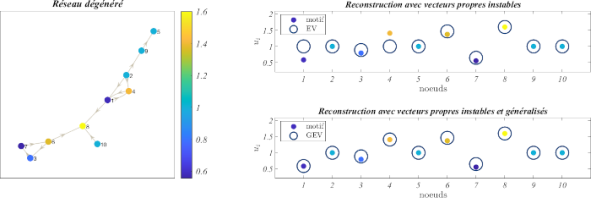
This dissertation therefore takes up the necessary foundations of Turing theory and reproduces the results established for networks. We then go beyond the framework already studied in the literature and consider degenerate networks, whose Laplacian matrix does not have an eigenvector basis, necessary for the theory. We then introduce a new formalism enabling the study of Turing theory on such a support. Secondly, we are also interested in pattern reconstruction. Indeed, while it has already been established that the pattern can be explained thanks to the eigenvectors of the Laplacian matrix associated with the unstable eigenvalues, we are especially interested in the effect of generalized eigenvectors in the reconstruction of the pattern.
2022 - "Popular science" category: François-Grégoire Biewart
Title: Study of a numerical method for approximating the basin of attraction of nonlinear dynamical systems by means of the Koopman operator
Promoter: Alexandre Mauroy
Summary:
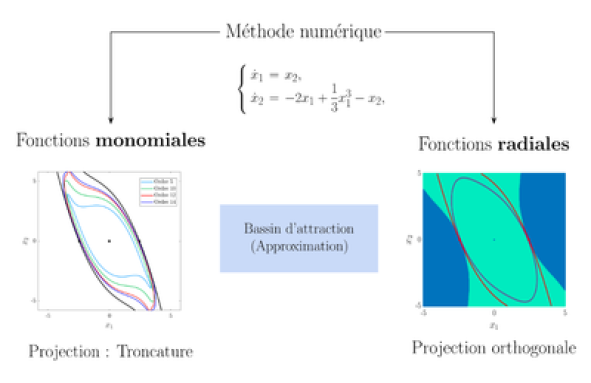
In the theory of nonlinear dynamical systems, the study of the global stability of fixed points is a far from obvious subject. Indeed, the stability of such attractors generally requires the determination of a particular Lyapunov function among an infinite number of possible choices, which can become quite tedious. This observation then motivates a functional approach to dynamical systems via the Koopman operator. In this context, the stability of fixed points relies on the existence of particular eigenfunctions of the operator whose support delimits the boundaries of the equilibrium basin of attraction. As this operator is infinite-dimensional, the analytical calculation of its eigenfunctions is unfortunately not trivial, and we generally have to determine an approximation on a finite subspace, generated by certain basis functions. In this case, the approximation of the eigenfunctions is obtained by calculating the eigenvectors of the matrix representation of the operator projected into the chosen basis. A natural basis often used in the literature is that of monomials, for which it is possible to characterize the approximation error between the exact and estimated eigenfunctions.
In this thesis, we investigate in particular the impact of projection and choice of basis on the approximation of the basin of attraction. To this end, we develop a general numerical method, which we apply with radial and monomial basis functions on various systems, notably in three dimensions. We show that the use of these functions provides a good estimate of the basin of attraction, in particular for radial basis functions not previously considered in this context. In parallel, we also address some theoretical issues arising from this study, leading in particular to rigorous stability guarantees, despite the approximations made.
2022 - "Scientific Excellence" category: Gaetan Louvet
Title : Robustness: influence function of scatter half-space depth and graphical lasso
Promoter: Germain Van Bever
Summary:
When we receive a dataset to analyze, outliers may appear, then impacting the statistical methods used. Various tools exist to assess the robustness of procedures, i.e. their sensitivity when data are contaminated. This article looks at the robustness of several statistical methods. In the first chapter, we begin by defining different tools for assessing robustness. We then introduce the best-known and most widely used robust estimators of position and dispersion. In the second chapter, we focus on depth functions, which quantify the centrality of a value for a certain parameter. In particular, we discuss position half-space and scatter depth. After introducing these various concepts, we derive the scatter depth influence function. We begin by considering that the position estimator on which the latter depends is known and fixed. We then turn to the case where the distribution is discrete with finite support, and finally conclude by giving bounds for the influence function in the case where the distribution is absolutely continuous with respect to the Lebesgue measure.
2021 - "Popular science" category: Célestine Hiernaux
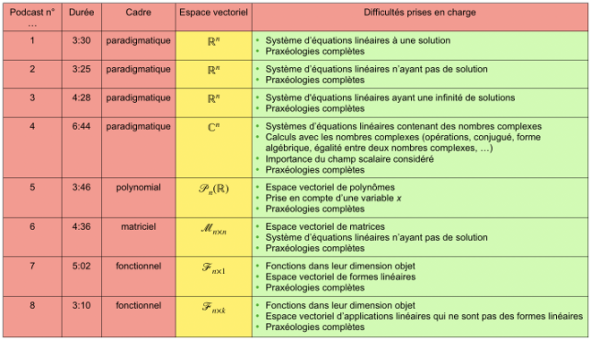
Title: Podcasts on linear combinations: Illustrating the unifying character of linear algebra... and much more!
Promoter: Martine De Vleeschouwer
Summary:
The unifying character of linear algebra is not easily identified by students new to the field. As part of this dissertation, we have created a device consisting of a proposed series of podcasts illustrating the algebraic notion of linear combination. This notion is elementary enough for beginners to be able to apply it to different vector spaces, in a progressive way, so as to highlight its unifying character. The specificities of teaching and learning linear algebra, such as the obstacle of formalism, mingle with the difficulties already identified in the literature. Some of these are dealt with in an evolving way by the device, such as difficulties in solving and interpreting systems of linear equations, working with complex numbers and considering functions as mathematical "objects", as elements of an algebraic structure. Justifying any technique used with a theoretical discourse is also often a problem for students in the transition from high school to university. All the podcasts therefore show the importance of theory and mathematical rigor in the exercises to facilitate learning in the field of linear algebra. This work of creating links between theory and exercises is often carried out independently by students. The podcasts, which would act as a complement to the lectures, could be useful to them. The system has been tested with students new to linear algebra, and surveys have been sent to them. Institutional constraints due to the organization of the implementation of the device and health constraints due to Covid-19 prevented a meaningful analysis of the results of these surveys. We also proposed one to the teaching assistants and collaborators of the exercise sessions for this test audience. The responses collected enabled us to obtain positive opinions on the project of this dissertation, to draw conclusions and to gather avenues for improvement and possible perspectives.
The project in video:
1. Linear combinations in R^n - video1
2. Linear combinations in R^n - video2
3. Linear combinations in R^n - video 3
4. Linear combinations in C^n
5. Linear combinations in Polynomials
6. Linear Combinations in Matrices
7. Linear Combinations in Applications - video1
8. Linear combinations in Applications - video2
2021 - "Scientific Excellence" category: Martin Baptiste
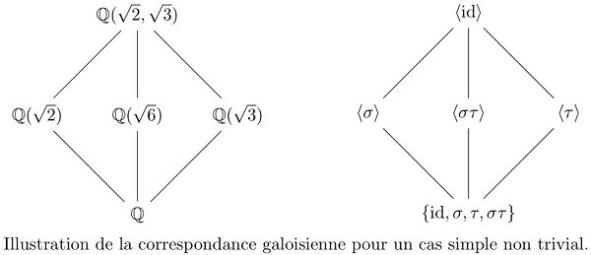
Title: Galois theory today.
Promoter: Alexandre Mauroy
Summary:
Galois theory in its modern form is often summarized in two theorems that have had a considerable influence on the way algebraic problems are approached. The first is Galois correspondence, and the second is the necessary and sufficient condition for solving a polynomial equation by radicals. Motivated by their effectiveness and depth, mathematicians have endeavored to generalize and transpose these theorems to other branches of mathematics. Thus, while the best-known applications of this theory seem somewhat outdated, today we find a remarkable diversity of new Galoisian correspondences offering a myriad of solutions and also problems open to the geometers of our time.
This dissertation is therefore intended more as a non-exhaustive summary of the various subjects in which Galois theory interferes than as a truly rigorous presentation of the whole theory. The first chapter is devoted to classical Galois theory, that developed by Galois, but in its modern form. It is more comprehensive than the following chapters, as it forms the basis for all those that follow. The aim is to provide a simpler presentation of this theory than can be found in books or well-known courses, and to demystify certain points for neophytes. In this way, I hope to present an approach that I would have liked to have read when I first came into contact with Galois theory. The second chapter deals with infinite Galois theory, a first extension of classical Galois theory to algebraic extensions of infinite degree. This theory, though important, is little discussed in books on Galois theory, and the aim of this section is to couple the somewhat abstract theory with some fairly concrete examples. The third shows the links between the arithmetic of extensions of the rational field and the associated Galois group. This chapter explains how Galois theory naturally applies to an older theory: number theory. The fourth chapter gives a brief introduction to differential Galois theory. This has many analogies with the first chapter, but the main focus of this section is the linear differential equation. The fifth chapter deals with the Galois theory of coverings, a theory which shows that there is a Galois correspondence between coverings and subgroups of the fundamental group of the basic topological space.
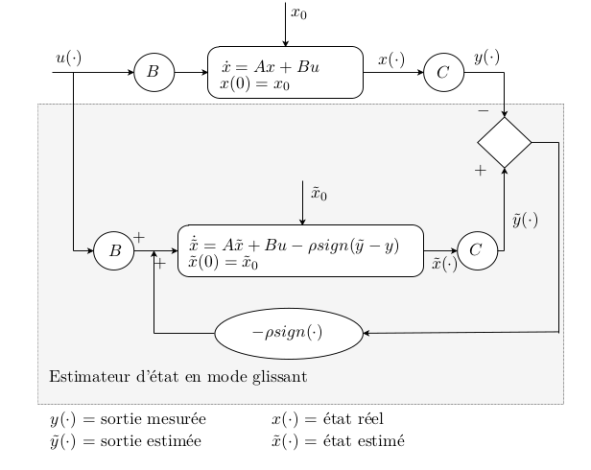
2020 - "Science popularization" and "Scientific excellence" categories: Judicaël Mohet
Title: Sliding mode estimation of the state of a linear convection-diffusion-reaction system.
Promoter: Joseph Winkin & Supervisor : Anthony Hastir
Summary:
Infinite-dimensional state estimation remains a real challenge to this day. The principle is to approximate the state trajectories of a dynamical system based on its input and output. In the case of an infinite-dimensional state space, it is also necessary to demonstrate the well-posedness of both the system and the estimator. One method of robust estimation is to apply a discontinuous input to the error dynamics, thereby trapping the trajectories in what is known as a sliding surface. This technique is known as sliding mode estimation, and its greatest advantage is that it can compensate for bounded disturbances acting on the system. In this thesis, such an estimator is applied in finite and infinite dimensions to a linear convection-diffusion-reaction model subjected to a bounded perturbation. The model describes the evolution of various industrial processes such as chemical or biochemical reactors. Using a functional approach, the well-posedness of the estimator is established by demonstrating the generation of a strongly continuous and compact semigroup on the Sobolev space H1(0,1). Stability is then proved using Lyapunov theory. Finally, a comparison of the estimator's performance in finite and infinite dimension is made using numerical simulations.
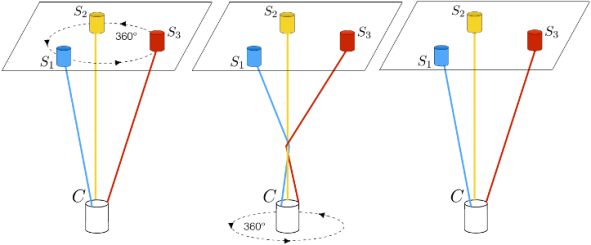
2019 - "Popular science" category: Hugo Henris
Title: Formation of the multi-wired satellite with adjoint satellites moving along Lissajous curves.
Promoter: Anne Lemaître
Summary:
In atmospheric physics and plasma geodesics, multi-point measurements are increasingly necessary. Even more so in the context of spatial interferometry, simultaneous measurements can be made using an array of probes connected by tethers aligned along the local vertical. In order to minimize fuel consumption, it has been devised to link these sensor-assisted satellites to a single satellite (rather than to each other) by means of cables. As rotation and gravitational force are not sufficient, the adjoining satellites are equipped with low-thrust engines afin order to keep the links between the satellites taut. This stabilizes the desired system dynamics. In this thesis, the complete modeling of the equations of motion of such a system is first detailed. One possible equilibrium is also presented, along with the effects of small deviations around it. A theoretical and numerical presentation of satellite motion along Lissajous curves is also given. The possibility of cable entanglement is obviously present, increasing the risk of collisions and the complexity of deploying such a system. This brief therefore contains an in-depth study of this risk. Firstly, by distinguishing two different types of entanglement (weak and strong), and secondly by identifying configurations more prone to risk than others, by means of theorem proving. A series of numbers of adjoint satellites and parameter values generating strong entanglements are then excluded. Finally, the study of the non-linearity effects of the motion of adjoint satellites along Lissajous curves, assumed to be unstable, is briefly presented.
Image source: H. Henris, Formation of the multi-wired satellite with adjoint satellites moving along Lissajous curves, Université de Namur, June 2019
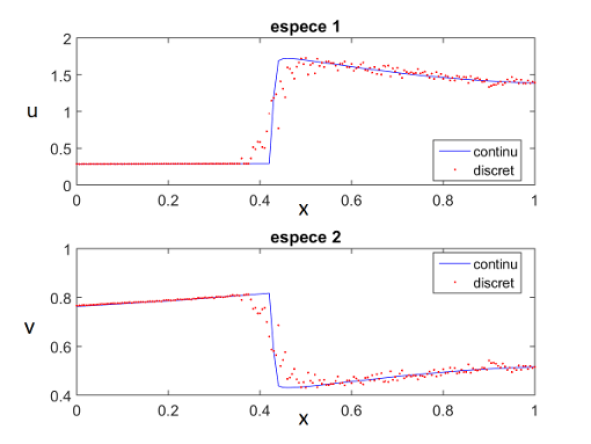
2019 - "Scientific Excellence" category: Alice Bellière
Title: Application of graph boundary theory to dynamical systems on reaction-diffusion type networks and Turing instability.
Promoter: Timotéo Carletti & Supervisor: Julien Petit
Summary:
Studying a network and the dynamics operating on it is of great interest since processes encountered in nature or technology can often be modeled by means of a network. However, the complexity of such networks, which are becoming ever larger, still prevents us from obtaining certain answers. Our research is based on graphon theory, which defines a boundary object that stores the network structure in memory. We apply this theory to the case of reaction-diffusion dynamics, including cases of Turing instability, where the stable reaction equilibrium is unstable for reaction-diffusion. We show that the solution on a network converges to that defined via a graph, offering us an alternative to introducing dynamics on a very large graph. We have applied the study of the convergence of the solution on a network to that via a graph to the case of a single species and then two interacting species following the Brusselator model (see figure below for an example). The graphon approach saves memory and execution time, and makes it easier to identify Turing patterns. Another advantage of the graphon approach is the relatively easy determination of the stability and eigenstructure of the corresponding graphon operator. As this operator is the infinite-dimensional analogue of the graph's Laplacian matrix, it allows us to avoid studying the eigenstructure of a high-dimensional matrix.
Image source: A. Bellière, Application de la théorie des limites de graphes aux systèmes dynamiques sur réseau de type réaction-diffusion et instabilité de Turing, Université de Namur, Juin 2019
2018 : Anthony Hastir
Title: Dynamical analysis of a nonisothermal axial dispersion reactor.
Promoter: J. Winkin
Summary:
Designing a control law to stabilize the temperature and concentration of chemical components during a reaction in a nonisothermal tubular reactor with axial dispersion still remains a challenge in the process engineering community. Preliminary steps such as characterization, stability analysis and equilibrium analysis of such a chemical reactor are therefore crucial. In this thesis, these steps are developed for a reaction of the type A -> B, where A represents the reactant and B the product. This type of distributed parameter system is governed by reaction-convection-diffusion partial differential equations with a nonlinear term. We first show that the system under study is well-posed by means of linear and non-linear semi-group theory in particular. Then, the exponential stability of the linear part is proved. The next step is equilibrium analysis, based on two specific numbers: the mass Peclet number and the thermal Peclet number. The analyses already carried out are extended to the case where these two numbers are different. The main result obtained is that the reactor can exhibit one or three equilibria, depending in particular on the diffusion coefficient. In addition, approximate analytical forms of the equilibrium profiles are calculated explicitly using perturbation theory. The final part of this thesis deals with the stability of equilibrium profiles. A linearized model around the various equilibria is constructed, and its well-posedness is demonstrated. Various approaches are used to study stability. In particular, a numerical method known as the Galerkin residual method is developed for equal Peclet numbers and extended to different Peclet numbers. All analyses and results obtained are supported by numerical simulations.
Image source: A. Hastir, Dynamical analysis of a nonisothermal axial dispersion reactor, Université de Namur, June 2018
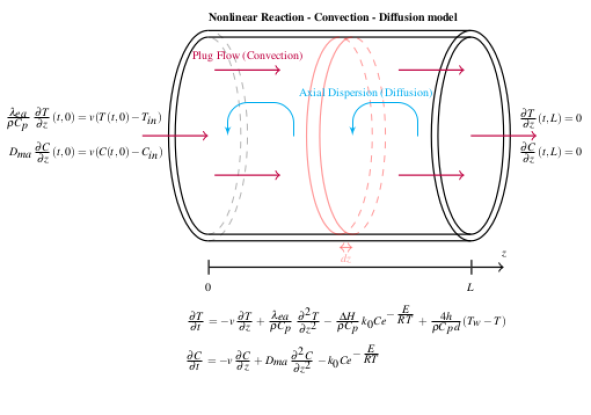
2017 - Arnaud Roisin
Title: Development of a symplectic integrator for binary systems. Application to the formation of giant planet systems.
Promoter: A.-S. Libert
Summary:
Currently, scientists estimate that more than half of all stellar systems are multiple. Exoplanets have already been detected in around sixty of these systems. In this thesis, we have developed a symplectic integrator to calculate the evolution of binary systems containing S-type planets, i.e. planets orbiting one of two stars. The advantage of such integrators is that, based on the Hamiltonian structure of the evolution equations, they can limit energy loss, even at high integration steps. Adapting the existing SyMBA code to binary systems required the introduction of an adapted set of coordinates, as well as a different Hamiltonian splitting. Our code is also adapted to the problem of close encounters between planets and close encounters between planets and the central body. The question of the migration of giant planet systems in binaries was then addressed. The code was modified to simulate type II migration of giant planets and to study the influence of a distant binary companion on the final configurations of the bodies. To do this, we studied the evolution of over 1,300 simulations. In particular, we focused on the influence of the initial parameters of the binary companion on the migration process.
Image source: A. Roisin, Développement d'un intégrateur symplectique pour les systèmes binaires. Application to the formation of giant planet systems., Université de Namur, June 2017
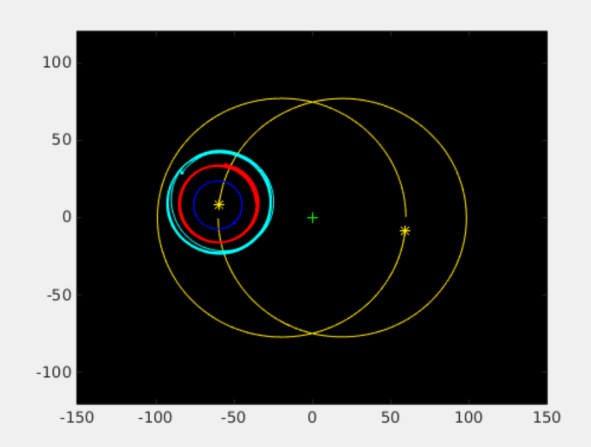
2016 : Elodie Mal & François Staelens
Elodie Mal
Title: Study of different mathematical formalisms in symplectic geometry and teaching design.
Promoter: A.-S. Libert
Summary:
Symplectic geometry is a mathematical discipline studying differentiable varieties equipped with a closed, nondegenerate 2-form. It applies perfectly to the study of phase spaces of conservative systems and can be studied according to three mathematical formalisms: dynamical systems, algebra and differential geometry. The Symplectic Geometry SMATB307 course taught to undergraduates in mathematical sciences at the University of Namur focuses on dynamical systems. The question of the relevance of offering a more differential geometry-oriented course naturally arises, and is the subject of this work. On the one hand, this thesis presents a theoretical study of symplectic geometry in different formalisms. Equivalent concepts in the dynamic, algebraic and differential formalisms are highlighted in order to discover the intertwining of the different axes. In addition, a course based on the differential formalism is designed. This teaching was offered to mathematical science students during the 2015-2016 academic year, and their opinions on the content of the session were analyzed via a questionnaire. This dissertation was written with a constant pedagogical concern.
Image source: F. Staelens, Etude des variétés hilbertiennes et application à la mécanique quantique, Université de Namur, June 2016
François Staelens
Title: Etude des variétés hilbertiennes et application à la mécanique quantique.
Promoter: A. Füzfa
Summary:
Infinite-dimensional differential geometry is not generally taught in university courses, but it is perfectly developed theoretically and globally. However, local writing and tensor calculus seem to have been sidelined in favor of global results. Hilbertian varieties, whose representation space is a separable Hilbert space, nevertheless seem to have the potential to play a role in theoretical physics. Quantum mechanics uses Hilbert spaces, while general relativity is based on Riemannian geometry. This motivates the study of Hilbertian varieties carried out in this thesis. A detailed presentation of the general concepts of infinite-dimensional differential geometry is given. In addition, this work takes a close look at local writing and tensor calculus. Most of the tensor formulas used in differential and Riemannian geometry are developed in the Hilbertian case. Finally, an attempted application to quantum mechanics is presented. This essay highlights a fundamental problem: quantum mechanics is profoundly linear, whereas differential geometry is inherently nonlinear. This dissertation is both a bibliographical study and an exploratory research.
Image source: F. Staelens, Etude des variétés hilbertiennes et application à la mécanique quantique, Université de Namur, June 2016

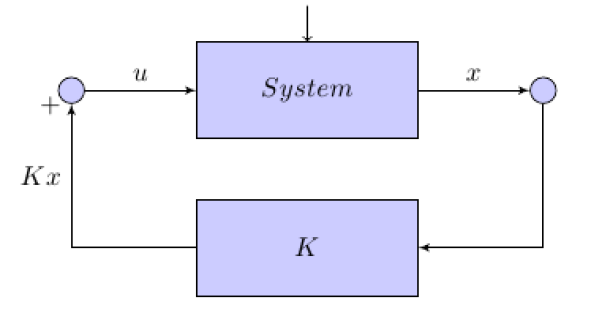
2015: François Lamoline
Title : LQ-optimal analysis and control of ported Hamiltonian systems.
Promoter: J. Winkin
Summary:
In this dissertation, we focus on infinite-dimensional ported Hamiltonian systems. This Hamiltonian port approach allows us to consider a wide range of problems involving control at the boundaries of the spatial domain. The main advantage of this Hamiltonian formulation is the structure of the resulting mathematical model. This allows us to develop a more appropriate analysis than the semi-group approach, which can be used for any infinite-dimensional dynamical system, but is difficult to implement in some cases.
Port Hamiltonian systems are dynamical systems on which the inputs act at the boundaries of the spatial domain. Outputs are also measured at the boundaries. We will show that it is possible to characterize inputs and outputs by matrices. These matrices will be used to study properties for this class of systems, such as the existence and uniqueness of a solution, stability, and to determine the equilibrium equation. We will also show that the class of Hamiltonian systems with ports is a subclass of spectral Riesz systems. Finally, we will study the linear quadratic control of a ported Hamiltonian system. Throughout this dissertation, we apply the theory presented to the example of a vibrating string.
Image source: F. Lamoline, Analysis and linear-quadratic optimal control of port-hamiltonian systems , report naXys-10-2015, University of Namur, August 2015
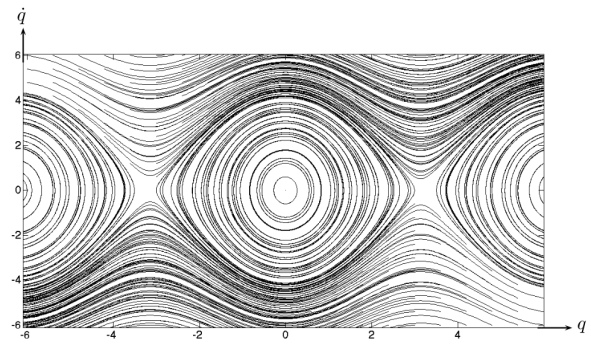
2014: Gwendoline Planchon & Manon Bataille
Gwendoline Planchon
Title: Pattern formation in biological models.
Promoter: T. Carletti
Summary:
Many patterns are present in nature and have prompted researchers to want to model pigmentation. The models used in this work consider systems of partial differential equations including the reaction-diffusion-advection process. Certain conditions enabling pattern formation were given by Alan Turing in 1952 and have since been called Turing instabilities. In this dissertation, we study reaction-diffusion-advection dynamics in continuous domains and then in networks (diffusion in d dimensional networks along d independent directions and diffusion in multiplexes) and determine the conditions to be imposed on the set of parameters to deal with Turing instabilities. We highlight the important role of domain discretization in the development or otherwise of spatially heterogeneous patterns. We also determine the set of bifurcation points giving three different types of patterns (stripes, rectangles and hexagons) for a given model. Finally, we show that coupling the levels of a multiplex allows the generation of Turing instabilities that are nevertheless not allowed on any of the layers taken separately.
Source : G. Planchon, Pattern formation in biological models, Université de Namur, June 2014
Manon Bataille
Title: Importance of relativistic and tidal effects in binary systems.
Co-sponsors: A. Lemaître & A.-.S. Libert
Summary:
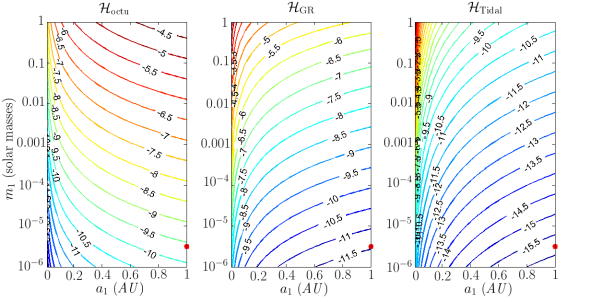
Binary star systems account for more than half of the star population. Recent observations have shown that some of them harbor an exoplanet. In this work, the long-term evolution of binary systems with a planetary or stellar companion is analyzed by means of octupole analytical development, to which relativistic and tidal (non-point masses) effects are added.
This approach accurately describes the dynamics of hierarchical triple systems, whatever the masses of the individual bodies. The aim of this study is to determine the importance of these two corrections in system dynamics. In particular, maps evaluating the orders of magnitude of each Hamiltonian contribution are developed for a wide range of masses and semi-major axes of the second body, in the case of conservative effects. The formation of binary systems is also addressed, with a view to understanding the accumulation of low-period planetary companions (between 1 and 10 days). A statistical study of the secular evolution of non-coplanar systems is carried out, taking into account both the orbital and spin evolution of the bodies. It follows that the combination of the Kozai mechanism and dissipative tides is responsible for the migration of planets to low periods.
Image source: M. Bataille, Importance of relativistic and tidal effects in binary systems, Université de Namur, June 2014

2014: Gwendoline Planchon & Manon Bataille
Gwendoline Planchon
Title: Pattern formation in biological models.
Promoter: T. Carletti
Summary:
Many patterns are present in nature and have prompted researchers to want to model pigmentation. The models used in this work consider systems of partial differential equations including the reaction-diffusion-advection process. Certain conditions enabling pattern formation were given by Alan Turing in 1952 and have since been called Turing instabilities. In this dissertation, we study reaction-diffusion-advection dynamics in continuous domains and then in networks (diffusion in d dimensional networks along d independent directions and diffusion in multiplexes) and determine the conditions to be imposed on the set of parameters to deal with Turing instabilities. We highlight the important role of domain discretization in the development or otherwise of spatially heterogeneous patterns. We also determine the set of bifurcation points giving three different types of patterns (stripes, rectangles and hexagons) for a given model. Finally, we show that coupling the levels of a multiplex allows the generation of Turing instabilities that are nevertheless not allowed on any of the layers taken separately.
Source : G. Planchon, Pattern formation in biological models, Université de Namur, June 2014
Manon Bataille
Title: Importance of relativistic and tidal effects in binary systems.
Co-sponsors: A. Lemaître & A.-.S. Libert
Summary:
Binary star systems account for more than half of the star population. Recent observations have shown that some of them harbor an exoplanet. In this work, the long-term evolution of binary systems with a planetary or stellar companion is analyzed by means of octupole analytical development, to which relativistic and tidal (non-point masses) effects are added.
This approach accurately describes the dynamics of hierarchical triple systems, whatever the masses of the individual bodies. The aim of this study is to determine the importance of these two corrections in system dynamics. In particular, maps evaluating the orders of magnitude of each Hamiltonian contribution are developed for a wide range of masses and semi-major axes of the second body, in the case of conservative effects. The formation of binary systems is also addressed, with a view to understanding the accumulation of low-period planetary companions (between 1 and 10 days). A statistical study of the secular evolution of non-coplanar systems is carried out, taking into account both the orbital and spin evolution of the bodies. It follows that the combination of the Kozai mechanism and dissipative tides is responsible for the migration of planets to low periods.
Image source: M. Bataille, Importance of relativistic and tidal effects in binary systems, Université de Namur, June 2014
2013 - Virginie Marelli
Title: Matching on school choice: theory and algorithms.
Promoter: T. Carletti, Co-promoter: G. Aldashev
Summary:
In this dissertation, we apply genetic algorithms to matching problems. Initially, we review the whole theory of matching, both from an economic and an algorithmic point of view. We analyze three matching problems: the simple case of one-to-one matching or marriage; unconstrained many-to-one matching and constrained many-to-one matching. In a second step, we briefly describe genetic algorithms, how they work and their adaptations. We integrate them into a simple matching problem: the marriage problem in order to test them. Then, we apply them to a real case of pupil allocation in Belgian schools. This problem is subject to constraints imposed by the "missions" decree. This case of many-to-one matching with constraints and indifferences has not yet been treated in the existing literature, and genetic algorithms give good results. Finally, we apply genetic algorithms to another matching problem: coalition formation. Here too, the contribution of these algorithms proves interesting.
Image source: V. Marelli, Matching on school choice: theory and algorithms, Université de Namur, June 2013
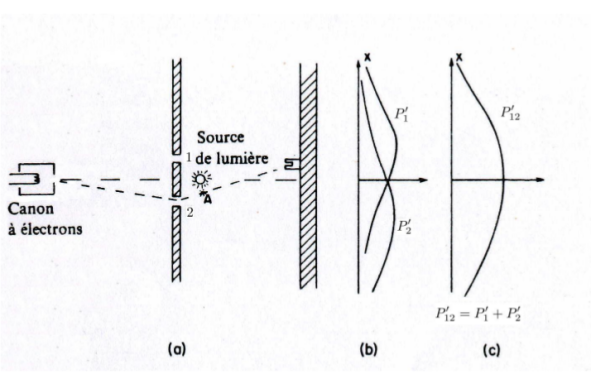
2012 - Estelle Collard
Title : Quantum mechanics: a study of the Schrödinger-Newton equations.
Promoter: A. FÜZFA
Summary:
This dissertation is intended as a study of the Schrödinger-Newton (SN) equations in the two-particle case. These SN equations were originally introduced by Penrose to replace the traditional Schrödinger equation and explain wavefunction decoherence at macroscopic scales. Penrose added gravitational self-interactions to quantum systems, by means of a Poisson equation, to force this decoherence.
Several studies have already investigated the solutions of the SN equations, but always in the case of a single particle. Some of their numerical results are reproduced in this thesis for the case of spherical symmetry. They show that there is a discrete infinity of stationary solutions associated with higher and higher energies. The fundamental solution has the lowest energy and no zero. Other papers have shown that this fundamental state is the only stable solution. In general, the n-th solution has n zeros and higher energy.
In this dissertation, the influence of mass has been studied and seems to confirm Penrose's hypothesis that the SN equations form a link between the quantum and macroscopic worlds. Indeed, the ground state, dimensioned according to mass, shows that heavy objects are extremely well localized, whereas quantum particles turn out to be non-localized. The transition between the quantum and macroscopic worlds occurs for masses of the order of 10-18 kg.
A study for two particles has been started in this thesis, although the expression of the SN equations for several particles is open to discussion. Two expressions are therefore studied here. The first, proposed especially for this thesis, is inspired by the center-of-mass decomposition of the Schrödinger equation, to which self-interactions are added. The second expression comes from the formulation of the SN equations proposed by Diosi; and this formulation has never been studied numerically for several particles. Both approaches were considered in the case of spherical symmetry. Various stationary solutions were found, associated with larger and larger energies; the solution with the lowest energy again being state and order of magnitude similar, although Diosi's expression presents a lower energy and a more localized state.
Finally, a study of the system with angular momentum was undertaken.
Image sources: R. Feynman, R. Leighton and M.Sands, Mécanique quantique , InterEditions, Paris, 1992
E. Collard, Quantum mechanics: a study of the Schrödinger-Newton equations, Université de Namur, June 2012
2011 - Romain Hendrickx
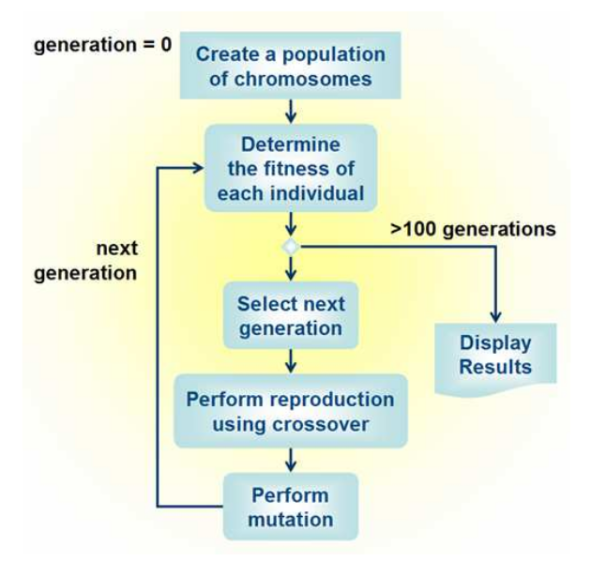
Title:Genetic algorithms: theory and applications.
Promoter: T. Carletti
Summary:
Genetic algorithms (GAs) are meta-heuristic solution methods for combinatorial optimization problems, whose operation is inspired by the evolutionary process described by Darwin.
The general idea is to compare the admissible solutions of the optimization problem with a set of individuals evolving in an abstract world, in which their adaptability is described by the objective function, in such a way that the greater the objective function, the more "adapted" the individuals are to their environment. Starting from a given initial population and simulating an evolutionary process based on alternating variation operators, enabling the space of admissible solutions to be explored, and a selection operator, enabling only the best individuals (i.e. those with the greatest fitness) to be retained, the evolutionary process can be based on the alternation of variation operators, enabling the space of admissible solutions to be explored, and a selection operator, enabling only the best individuals (i.e. those with the greatest fitness) to be retained. The aim of this dissertation is to provide an overview of how genetic algorithms work in general. The first part of the dissertation is devoted to introducing the general structure of GAs, with the most common specifications for variation and selection operators (Chapters 1 and 2), as well as a theoretical justification for their use (Chapter 3). The second part of the dissertation is devoted to the application of GAs to certain combinatorial optimization problems. For example, we study the optimal strategy problem of a robot whose task is to clean a surface covered with empty cans (known as "Robby, the Soda-Can-Collecting Robot", Chapter 4). We also consider the robust optimization of event-based experiments in the context of functional magnetic resonance imaging (carried out as part of the Master 2 internship, Chapter 5).
Image source: Source: R. Hendrickx, Les algorithmes génétiques : théorie et applications , Université de Namur, June 2011