Il récompense la qualité d’un travail de recherche dans les mathématiques et leurs applications, qui se distingue particulièrement par son originalité, la profondeur et la rigueur de son propos, la portée des résultats obtenus et leur caractère applicable ou publiable. Une importance particulière est accordée à la personnalité des candidats, leur maturité, leur charisme, leur implication personnelle dans le travail scientifique et leur aptitude à présenter les résultats d’une manière claire et adaptée face à un public non spécialisé.

Curriculum Vitae de Frank Callier.

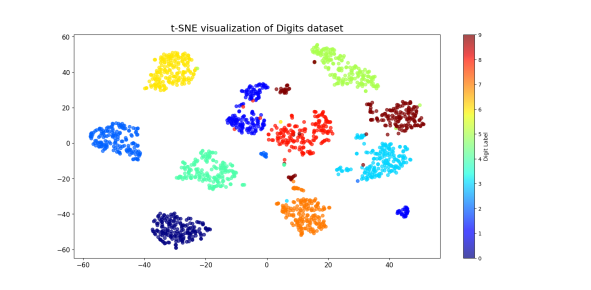
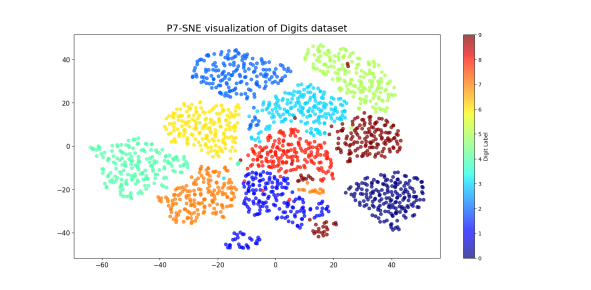
Titre : Visualisation de données complexes : repenser la loi de distribution de la méthode t-SNE

Promotrice : Anne-Sophie Libert

Co-promoteur : Benoît Frenay

Résumé :

Dans le cadre de mon mémoire de recherche, j’ai choisi de m’attaquer à une hypothèse rarement remise en question dans la littérature scientifique : l’utilisation systématique de la loi t de Student dans l’algorithme t-SNE, une méthode aujourd’hui incontournable pour la visualisation de données complexes. L’objectif de mon travail a été de réévaluer ce choix fondamental, à la fois sur le plan théorique et empirique, en interrogeant son bien-fondé et en explorant des alternatives potentiellement plus adaptées à certaines structures de données.

Pour cela, j’ai proposé de remplacer la loi t par trois autres distributions aux propriétés contrastées : la log-normale, la loi de Pearson de type VII et la de Weibull. Ces choix ne sont pas arbitraires : chacun modifie différemment les forces d’attraction et de répulsion dans l’espace projeté, ce qui affecte directement la qualité de la visualisation obtenue. J’ai évalué ces modifications à l’aide de trois métriques complémentaires, sur trois jeux de données bien connus : Iris, Digits et un sous-échantillon de MNIST. Les résultats ont montré que certaines paramétrisations alternatives surpassaient la version classique de t-SNE selon plusieurs critères quantitatifs. Toutefois, ce travail a aussi mis en lumière un décalage fréquent entre les performances mesurées et la qualité visuelle perçue, ce qui souligne la complexité intrinsèque de l’évaluation en visualisation.

Une autre contribution de ce mémoire réside dans l’analyse fine des forces sous-jacentes à ces méthodes. En modélisant leur rayon d’influence, j’ai mis en évidence que la version classique de t-SNE agit très localement, tandis que les distributions alternatives induisent des interactions plus globales. Cette différence structurelle pourrait expliquer certaines variations de comportement observées, même si un lien rigoureux entre ces forces et les performances reste encore à établir.