Mathématique études

Votre bachelier démarre par une solide formation en mathématiques générales (logique, analyse, algèbre, géométrie et probabilités). 

Rapidement, vous êtes confrontés à des questions actuelles de mathématiques appliquées à travers des cours de spécialisation en optimisation, contrôle, statistiques, réseaux et systèmes dynamiques. 

Votre formation est ouverte à d’autres disciplines telles que l’économie, la gestion, l’informatique et les sciences. Vous pouvez d’ailleurs, en fin de bachelier en sciences mathématiques, accéder facilement à des masters d’autres disciplines (masters en informatique et en sciences économiques). 

Tout au long du bachelier, vous recevez une formation poussée en programmation scientifique et vous développez votre compréhension de l’anglais pour lire et écrire des articles scientifiques. 

Une dimension humaine complète votre bachelier par une approche réflexive sur le rôle et l’impact des sciences dans la société. 

Sciences études

Vous partez sur de bonnes bases

  • vous aimez manipuler les formules ; 
  • vous vous sentez à l’aise en mathématiques ; 
  • vous faites preuve de rigueur et d’abstraction dans vos raisonnements ;
  • vous aimez résoudre des problèmes concrets. 

Méthodes d’enseignement

Cours, séances d’exercices, travaux pratiques, ateliers de programmation informatique… tout est mis en œuvre pour assurer votre maîtrise des concepts et développer vos compétences de communication, d’autonomie, d’organisation, de travail en équipe, d’inventivité, d’esprit critique et de recherche scientifique. 

Organisés en petites équipes (3 à 5 étudiants) et encadrés par un assistant, les travaux de groupe vous permettent d’approfondir une partie de la matière par vous-mêmes. 

Grâce au projet « étudiant-chercheur », vous pouvez vous initier à la recherche sous la supervision d’un chercheur du département. Cette expérience vous permet aussi de développer votre autonomie, votre créativité et votre sens critique. 

Sciences études

Parmi nos projets pédagogiques innovants, vous réalisez, dans le cadre du cours d’Astronomie, des soirées d'observation depuis la coupole de l'Observatoire astronomique Antoine Thomas situé au centre du campus. Vous construisez un projet d’observation que vous présentez comme s’il s’agissait d’une animation pour le grand public. 

Vous complétez votre formation par la réalisation d’un travail interdisciplinaire. Ce projet lié aux mathématiques appliquées comprend une partie personnelle de recherche et de rédaction suivie d’une partie collective. Expositions, conférences, jeux interactifs, rédactions de journaux, ce projet prend des formes multiples et tend à développer votre esprit d’initiative, votre sens de l’organisation et vos aptitudes de communication orale et écrite.  Les travaux réalisés sont présentés dans le cadre du Printemps des Sciences. 

Aides à la réussite

Réussir une année d’études à l’université implique de nombreux défis. 

Pour vous aider à les relever, l’UNamur vous accompagne dans le développement de vos compétences disciplinaires, méthodologiques, humaines… avec le soutien de nombreux professionnels. 

Cours préparatoires, aide individualisée… Découvrez les dispositifs mis en place pour votre formation. 

Découvrir les aides à la réussite en mathématique

Après le bachelier : le master

L’Université de Namur organise :  

directement accessibles après l’obtention de votre diplôme de bachelier en sciences mathématiques. 

Si vous avez acquis les crédits de l’option « économie et gestion » durant votre bachelier en mathématique, vous pouvez accéder aux masters en économie de l’Université de Namur. 

Si vous avez acquis les crédits de l’option « programmation scientifique » durant votre bachelier en mathématique, vous pouvez accéder aux masters en informatique de l’Université de Namur. 

Suite à la mise en service d'une nouvelle application pour la gestion des programmes d'enseignement, certaines données n'apparaissent pas encore sur cette page. Vous trouverez l'affichage complet de la formation sur https://directory.unamur.be/teaching/programmes/200B

Tout replier
Tout déplier
Tout replier
Tout déplier
Tout replier
Tout déplier
Tout replier
Tout déplier

Conditions d'admission

Peuvent être admis aux études de bachelier, les titulaires d’un des titres suivants :
  • soit du certificat d'enseignement secondaire supérieur délivré à partir de l'année scolaire 1993-1994 par un établissement d'enseignement secondaire de plein exercice ou de promotion sociale de la Communauté française ainsi que les titulaires du même certificat délivré, à partir de l'année civile 1994, par le jury de la Communauté française (1);
  • soit du certificat d'enseignement secondaire supérieur délivré au plus tard à l'issue de l'année scolaire 1992-1993 accompagné du diplôme d'aptitude à accéder à l'enseignement supérieur (2);
  • soit d'un diplôme délivré par un établissement d'enseignement supérieur de la Communauté française sanctionnant un grade académique, soit d'un diplôme délivré par une institution universitaire ou un établissement organisant l'enseignement supérieur de plein exercice en vertu d'une législation antérieure (3) ;
  • soit d'un diplôme d'enseignement supérieur délivré par un établissement d'enseignement de promotion sociale (4);
  • soit d'une attestation de succès à un des examens d'admission organisés par les établissements d'enseignement supérieur ou par un jury de la Communauté française ; cette attestation donne accès aux études des secteurs, des domaines ou des cursus qu'elle indique ;
  • soit d'un diplôme, titre ou certificat d'études similaire à ceux mentionnés aux litteras précédents délivré par la Communauté flamande, par la Communauté germanophone ou par l'Ecole royale militaire ;
  • soit d'un diplôme, titre ou certificat d'études étranger reconnu équivalent à ceux mentionnés aux litteras précédents (1) à (4) ;
  • soit du diplôme d'aptitude à accéder à l'enseignement supérieur (DAES) conféré par le jury de la Communauté française ;
  • soit d'une décision, prise par le Gouvernement de la Communauté française de Belgique, attestant de l'équivalence du niveau d'études réalisées à l'étranger à un niveau d'études sanctionnées par l'octroi d'un grade académique de la Communauté française.

Sous certaines conditions, l’étudiant peut obtenir une réduction de la charge d’enseignement (jusqu’à 120 crédits maximum).

Pour plus d’informations, il y a lieu de prendre contact avec le service des inscriptions.

 

Description

Le bachelier démarre par une solide formation en mathématiques générales (logique, analyse, algèbre, géométrie et probabilités).

Rapidement, les étudiants sont confrontés à des problématiques actuelles en mathématiques appliquées à travers des unités d’enseignement (UE) de spécialisation en optimisation, contrôle, statistiques, réseaux, mécanique et systèmes dynamiques.

La formation est ouverte à d’autres disciplines dans lesquelles les mathématiques se développent : l’économie, la gestion, l’informatique et les sciences. Dès le bloc 1, les étudiants peuvent choisir des UE dans ces différentes disciplines pour panacher leur programme. Les étudiants peuvent d’ailleurs, en fin de bachelier en sciences mathématiques, accéder facilement (avec des passerelles raisonnables) à des masters d’autres disciplines (masters en Informatique et en Sciences économiques).

Tout au long du bachelier, les étudiants reçoivent une formation poussée en programmation scientifique et développent leur compréhension de l’anglais pour lire et écrire des articles scientifiques.

Une dimension humaine complète la formation de bachelier par une approche réflexive sur le rôle et l’impact des sciences dans la société, les mathématiciens étant appelés à appliquer leurs connaissances à des contextes très divers de la vie de la société.

 

Aide à la réussite

L’Université de Namur (UNamur) souhaite faciliter la transition entre l’enseignement secondaire et l’université. Différents dispositifs pédagogiques sont mis en place pour aider les étudiants au cours de leurs études.

  • Passeport pour le bac

En début de bloc 1, les étudiants sont invités à répondre à un questionnaire appelé « Passeport » qui leur permet de se situer par rapport aux attentes des enseignants et par rapport aux autres étudiants. Sur base des résultats, les étudiants peuvent bénéficier de séances de correction et de renforcement des prérequis. Ces « passeports » sont réalisés à partir d’une recherche menée au départ de l’Université de Namur pour cerner les « prérequis » nécessaires lors de l’entrée à l’université, c’est-à-dire les aptitudes acquises dans le secondaire, auxquelles les unités d’enseignement de bloc 1 font appel.

  • Séminaire de méthodologie du travail étudiant

Dès le début du bloc 1, les étudiants doivent se familiariser avec de nouvelles techniques d’apprentissage : prendre des notes exhaustives d’exposés denses, gérer leur temps de travail en se fixant leurs propres échéances intermédiaires, mémoriser des quantités de matières plus importantes que dans le secondaire, les résumer et les synthétiser. Ils doivent assurer leur compréhension des textes liés aux différentes matières et se familiariser à un type de communication propre à l’université. Disposer de stratégies efficaces dans ces domaines constitue un atout majeur pour réussir une première année.

Un séminaire de 5 séances de méthodologie vise à préparer les étudiants à ces nouvelles techniques d’apprentissage.

Par ailleurs, la Cellule interfacultaire d’appui pédagogique (CIAP) de l’UNamur répond à toute demande d’aide méthodologique et peut assurer un suivi individuel tout au long de l’année.

  • Remédiation

Dès la première semaine de cours et pendant tout le bloc 1, des séances de remédiation sont organisées et intégrées à la formation : c’est l’opération « Labo math ».

Les délégués de cours relayent auprès des enseignants les difficultés rencontrées par les étudiants. Des séances de remédiation et d’exercices sont alors proposées pour les contenus des UE moins bien compris par les étudiants. Concrètement, chaque mercredi, une partie de la matinée est consacrée à la révision des principales matières scientifiques et à la méthodologie du travail universitaire.

  • Disponibilité permanente et contact direct

La proximité des étudiants et des enseignants qui caractérise le département de mathématique et l’UNamur permet un apprentissage personnalisé et attentif. Une question posée par email reste rarement sans réponse, un contact s’établit très facilement pour une demande d’explications complémentaires, avec les professeurs et assistants. Les étudiants sont connus, écoutés, conseillés et encadrés, s’ils le souhaitent. Le département de mathématique offre à ses étudiants cette présence et cette interaction permanente, permettant à chacun d’évoluer à son propre rythme, avec un programme personnalisé, suivant ses centres d’intérêt et son projet de vie.

 

Méthodes d'enseignement

Théorie, séances d’exercices, travaux pratiques, ateliers de programmation informatique… tout est mis en œuvre pour que les étudiants maîtrisent les concepts et développent leurs compétences de communication, d’autonomie, d’organisation, de travail en équipe, d’inventivité, d’esprit critique et de recherche scientifique.

Organisés en petites équipes (3 à 5 étudiants) et encadrés par un assistant, les travaux dirigés et les travaux de groupe permettent aux étudiants d’approfondir une partie de la matière et de se familiariser avec le travail en équipe.

Grâce au projet « étudiant-chercheur », les étudiants peuvent s’initier à la recherche sous la supervision d’un chercheur du département. Cette expérience leur permet aussi de développer leur autonomie, leur créativité et leur sens critique.

Parmi nos projets pédagogiques innovants, les étudiants réalisent, dans le cadre du cours d’Astronomie, des soirées d'observation depuis la coupole de l'Observatoire astronomique Antoine Thomas situé au centre du campus. Ils construisent un projet d’observation qu’ils présentent comme s’il s’agissait d’une animation pour le grand public.

Les étudiants complètent leur formation par la réalisation d’un travail interdisciplinaire. Ce projet lié aux mathématiques appliquées comprend une partie personnelle de recherche et de rédaction, suivie d’une partie collective. Expositions, conférences, jeux interactifs, rédactions de journaux, ce projet prend des formes multiples et tend à développer leur esprit d’initiative, leur sens de l’organisation et leurs aptitudes de communication orale et écrite. Les travaux réalisés sont présentés dans le cadre du Printemps des Sciences.

 

Finalités et objectifs

Au terme du bachelier en sciences mathématiques, les étudiants maîtriseront les compétences suivantes :

  1. Objectifs généraux
  • maîtriser des savoirs fondamentaux en mathématiques dans les domaines de l’algèbre et de la géométrie, de l’analyse, des probabilités et de la statistique, et de la programmation ;
  • faire preuve d’ouverture vers d’autres disciplines telles que l’économie ou la gestion, la physique, la biologie, la sociologie... ;
  • mobiliser leurs savoirs et transférer leurs connaissances d’une situation à l’autre, d’un domaine à l’autre ou encore d’une discipline à l’autre ;
  • développer leur capacité de raisonnement et d’abstraction, la nécessité du recours à un langage et une démarche de pensée rigoureuse dans une démarche scientifique ;
  • rédiger des textes scientifiques en anglais et être capables de comprendre la littérature scientifique du domaine ;
  • acquérir une autonomie de plus en plus grande.
  1. Objectifs spécifiques à l’orientation vers les mathématiques appliquées à l’UNamur :
  • être confrontés aux différents domaines d’application des mathématiques ;
  • réinvestir, en situation, les acquis relatifs aux savoirs fondamentaux ;
  • traiter des données réelles souvent complexes et recourir à l’outil informatique ;
  • développer des compétences en différents langages de programmation (C, Matlab, Python…) et d’écriture scientifique (LaTeX...).

 

Évaluation

  • En bloc 1

En bloc 1, des évaluations formatives sont organisées fin octobre dans certaines matières. Les enseignants corrigent les copies, les commentent et organisent des séances de correction collectives. Ces tests n’interviennent pas dans les notes qui seront attribuées en fin d’année. Il s’agit uniquement d’un outil de formation pour que les étudiants puissent se rendre compte du niveau d’exigence des enseignants et juger de l’efficacité de leur travail et de leur aptitude à gérer une situation d’examen.

Une aide personnalisée ou en petits groupes est également offerte aux étudiants afin d’analyser les résultats obtenus aux évaluations formatives, de discuter de la méthode de travail ou d’approfondir certaines parties d’une matière.

En janvier, les étudiants de bloc 1 présentent les examens sur les matières enseignées lors du 1er quadrimestre. En cas d’échec, les étudiants pourront présenter l’examen concerné en juin et en août-septembre.

Les étudiants sont invités à lire attentivement, pour chaque activité d’apprentissage, les modalités prévues par les enseignants pour chaque examen. Il est fréquent de présenter un écrit d’exercices et un oral plus théorique pour une même UE, mais le poids respectif des deux épreuves peut varier. D’autres types d’évaluation sont également présents : une évaluation continue (comme l’anglais), un rapport ou un travail personnel, une présentation collective, un logiciel à utiliser…

  • Au-delà du bloc 1

Au-delà du bloc 1, les étudiants présentent en janvier les examens des UE suivies au premier quadrimestre et en juin, celles du second quadrimestre uniquement ; en cas d’échec, en janvier ou en juin, les examens peuvent être représentés en août-septembre. Plusieurs types d’évaluation sont possibles comme en bloc 1.

 

Les métiers des mathématiciens

Métiers des mathématiciens

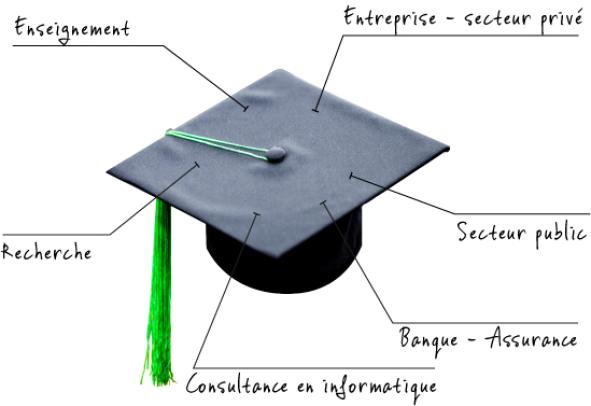
Pour les diplômés en mathématiques appliquées de l’Université de Namur, la transition études-monde du travail ne présente pas de difficulté majeure : les écoles manquent de professeurs de mathématiques ; le monde de l’entreprise recherche des compétences en réseaux, systèmes dynamiques, optimisation, contrôle, modélisation et programmation, autant d’atouts que possèdent les mathématiciens formés à l’UNamur. 

Confronter les mathématiques au réel 

De nombreux mathématiciens investissent leurs connaissances au sein des entreprises. Beaucoup de secteurs d’activités apprécient leur esprit d’analyse et de synthèse ainsi que leur rigueur. Que ce soit dans la consultance ou le monde économique et industriel, les mathématiciens ont largement leur place pour modéliser des phénomènes et des situations et plus largement mettre leur bagage mathématique au service de la société. 

Bâtir des solutions informatiques 

Les mathématiciens de l’UNamur reçoivent une solide formation en programmation scientifique, acquis que beaucoup valorisent au sein de diverses organisations (privées ou publiques), ou dans des sociétés de services informatiques. Après quelques années en développement d’applications, les mathématiciens évoluent généralement vers la gestion de projets. 

Quels que soient l’intitulé de leur fonction et leur niveau de responsabilité, ils œuvrent à faire interagir harmonieusement l’être humain et un système de gestion et de traitement de l’information… un défi permanent qui exige un bon sens des relations interpersonnelles et une excellente connaissance des technologies et du monde de l’entreprise. 

 Mon travail d’IT manager s’apparente par moment à une démonstration mathématique. Je pars d’une hypothèse, c’est-à-dire l’existant, le budget, les ressources et je dois aboutir à une thèse, en l’occurrence un gros projet business, par exemple installer une société à l’étranger. Pour y aboutir, je mène une véritable démonstration à l’aide de lemmes, c’est-à-dire des petites implémentations de solutions informatiques. Pour installer une société à l’étranger, il faut par exemple passer par la sécurisation de son réseau informatique. 

Alain Dieudonné, IT Manager

Évaluer des risques financiers ou économiques 

La gestion du risque est un enjeu stratégique dans les organismes bancaires et financiers, les places boursières, les compagnies d’assurances, mais aussi les institutions parastatales de sécurité sociale, de contrôle des pensions, etc. Grâce à leurs bonnes connaissances en modélisation, les mathématiciens exercent souvent des fonctions liées au contrôle de l’incertitude inhérente à la plupart des activités économiques.

Produire des statistiques 

Les statistiques jouent un rôle important dans la société actuelle : sondages d’opinion et enquêtes font partie de notre quotidien. Certains bureaux d’études spécialisés dans la conduite de ce type d’analyse font appel aux mathématiciens. 

Modéliser la réalité 

Que ce soit pour la forme des lentilles de contact, la dynamique d’une population, la concentration des débris spatiaux, les mouvements des océans, la compréhension des réseaux sociaux, le travail des mathématiciens est toujours lié à une modélisation : être capable de comprendre, simplifier, conceptualiser et visualiser une situation, pour en sortir un modèle plus abstrait et susceptible de fournir une description globale d’un phénomène. 

Je travaille depuis quelques années comme actuaire dans une société de consultance dans le domaine des pensions complémentaires. Nous vivons dans un monde rempli d’aléas : le rôle de l’actuaire est de quantifier, de modéliser les incertitudes… Les mathématiques permettent avant tout de développer notre manière de penser, ce qui fait de notre capacité d’analyse notre principal outil de travail. 

Noémie Laloux, actuaire 

Transmettre la passion du réel 

L’enseignement et le monde de la formation représentent toujours un des débouchés importants pour les mathématiciens. Près d’un tiers de nos jeunes diplômés actifs professionnellement communiquent leur passion du réel en enseignant les mathématiques et/ou les sciences dans l’enseignement secondaire supérieur, dans les hautes écoles et à l’université. 

La matière que l’on enseigne n’est pas particulièrement difficile. Il faut surtout donner le goût des mathématiques aux jeunes et faire comprendre les maths à celles et ceux qui ont des difficultés. C’est un défi quotidien. 

Marie Matelart, Professeur de mathématiques en école secondaire 

Repousser les limites de nos connaissances 

Les mathématiciens poursuivent des recherches essentiellement en milieu académique, en Belgique ou à l’étranger. Les universités et des fonds publics (FNRS, FRIA, etc.) financent la réalisation d’un doctorat (entre 4 et 6 ans) ou octroient des bourses limitées dans le temps pour la participation à un programme de recherche, parfois en partenariat avec le monde de l’entreprise. 

À côté de la recherche fondamentale, les mathématiques sont souvent un outil précieux pour le progrès scientifique dans d’autres disciplines : informatique, astrophysique et physique, météorologie, économie, transport, biologie… Dans ces contextes pluridisciplinaires, les doubles compétences représentent souvent un atout. 

Sciences études